Vinkel mellem vektorer

Indhold

Vinklen mellem to vektorer i planen

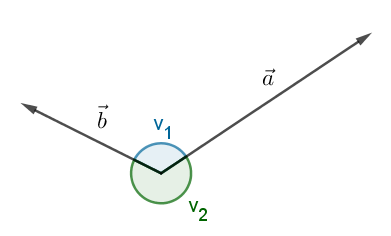
Når to vektorer afsættes i samme punkt, så danner vektorerne to vinkler. På figuren herover har vi kaldt de to vinkler v1 og v2.

Den mindste af de to vinkler omtales som vinklen mellem vektorerne. På figuren herover er v1 vinklen mellem vektorerne $\vec{a}$ og $\vec{b}$ .

Vinklen mellem to vektorer ligger altid i intervallet fra 0° til 180°.

Sætning. Sammenhængen mellem skalarproduktet og vinklen mellem vektorerne.

Der er følgende sammenhæng mellem skalarproduktet af to vektorer $\vec{a}$ og $\vec{b}$ og vinklen v mellem vektorerne:

$\vec{a} \cdot \vec{b} = | \vec{a} | \cdot | \vec{b} | \cdot \cos(v)$

Dvs. at

$\cos(v) =\frac{\vec{a} \cdot \vec{b}}{| \vec{a} | \cdot | \vec{b} |}$

To vektorer er givet ved

$\begin{align*} \vec{u} &= \binom{-4}{8} \\[1em] \vec{w} &= \binom{3}{6} \end{align*}$

Vi vil bestemme vinklen mellem $\vec{u}$ og $\vec{w}$ .

Vi bestemmer først skalarproduktet:

$\begin{align*} \vec{u}\cdot \vec{w} &= -4 \cdot 3 + 8 \cdot 6 \\[1em] &= -12 + 48 \\[1em] &= 36 \end{align*}$

Derefter bestemmer vi længden a...