Grundlæggende begreber

Vektor

• En vektor er et objekt, der både har en størrelse og en retning.
• En vektor noteres med et lille eller to store bogstaver med en pil over, fx  eller .
• Vektorer repræsenteres geometrisk med pile. Du kan se nogle eksempler herunder:

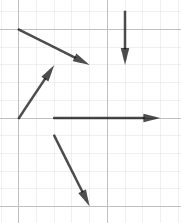
• En vektor beskrives med koordinater eller en længde og en retningsvinkel. Fx har nedenstående vektor  længden 5 og retningsvinkel 53,1°, mens koordinaterne er

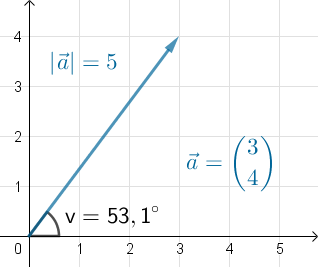
Nulvektor

• Nulvektoren er vektoren med længden 0. Nulvektoren er givet ved

• Nulvektoren er en ugentlig vektor, da den har længden 0.

Egentlig vektor

• En egentlig vektor er en vektor, der ikke er nulvektoren.

Uegentlig vektor

• En uegentlig vektor er en vektor med længden 0, dvs. nulvektoren.

Enhedsvektor

• En enhedsvektor er en vektor med længden 1. Enhedsvektoren   med retningsvinkel v er givet ved

• Hvis  er en egentlig vektor, så er enhed