Beviser med vinklen mellem to vektorer

Indhold

Skalarprodukt og vinklen mellem vektorer
Spids, ret eller stump vinkel
Skalarproduktet er 0, hvis og kun hvis vektorerne er ortogonale

Skalarprodukt og vinklen mellem vektorer

Sætning. Sammenhængen mellem skalarproduktet og vinklen mellem vektorerne.

Der er følgende sammenhæng mellem skalarproduktet af to vektorer $\vec{a}$ og $\vec{b}$ og vinklen v mellem vektorerne:

$\vec{a} \cdot \vec{b} = | \vec{a} | | \vec{b} |\cos(v)$

Dvs. at

$\cos(v) =\frac{\vec{a} \cdot \vec{b}}{| \vec{a} | | \vec{b} |}$

Læs mere om skalarprodukt og vinkler på siden Vinkel mellem vektorer.

Bevis

Få forklaringer til alle udregningerne ved at holde musen over lighedstegnene og pilene.

Beviset for sætningen består af to dele: Først beviser vi, at sætningen gælder, når $\vec{a}$ og $\vec{b}$ ikke er parallelle. Derefter beviser vi, at sætningen også gælder, når $\vec{a}$ og $\vec{b}$ er parallelle.

Vi antager først, at vektorerne ikke er parallelle

Da $\vec{a}$ og $\vec{b}$ ikke er parallelle, så danner de en vinkel v, når vi afsætter dem i samme punkt:

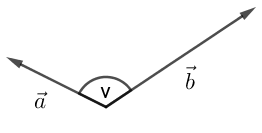
Vi tilføjer vektoren $\vec{a}-\vec{b}$ :

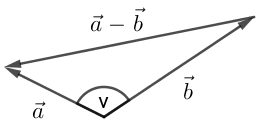
De tre vektorer danner en trekant med sidelængderne $|\vec{a}|$ , $|\vec{b}|$ og $|\vec{a}-\vec{b}|$ . Vi kan beskrive sammenhængen mellem sidelængderne med cosinus-relationen:

$|\vec{a}-\vec{b}|^2 = |\vec{a}|^2 + |\vec{b}|^2 - 2 \cdot |\vec{a}| \cdot |\vec{b}| \cdot \cos(v)$

Vi omskriver nu $|\vec{a}-\vec{b}|^2$ ved at benytte regnereglerne for skalarprodukt:

(\vec{a}-\vec{b}) \cdot (\vec{a}-\vec{b})

Ved at ...

$\|\vec{a}-\vec{b}\|^2$	=	$(\vec{a}-\vec{b}) \cdot (\vec{a}-\vec{b})$

	=	$\vec{a} \cdot \vec{a} - \vec{a} \cdot \vec{b} - \vec{b}\cdot \vec{a} + \vec{b}\cdot \vec{b}$

	=	$\vec{a} \cdot \vec{a} - \vec{a} \cdot \vec{b} - \vec{a}\cdot \vec{b} + \vec{b}\cdot \vec{b}$

	=	$\|\vec{a}\|^2- 2\vec{a} \cdot \vec{b}+ \|\vec{b}\|^2$

	=	$\|\vec{a}\|^2 + \|\vec{b}\|^2- 2 \vec{a} \cdot \vec{b}$