Vektorer i planen

Vektorer i planen

[37]

Projektion af vektor på vektor

Indhold

Hvad er vektorprojektion?
Bestem projektionsvektoren
Længden af projektionsvektoren
- Eksempel: Bestem længden af projektionsvektoren
Opgaver om vektorprojektion

Hvad er vektorprojektion?

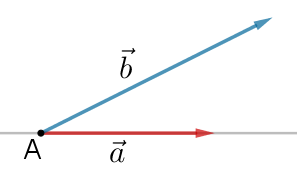
På figuren herover ses to vektorer $\vec{a}$ og $\vec{b}$ afsat i punktet A. Vi vil bestemme projektionen af $\vec{b}$ på $\vec{a}$ .

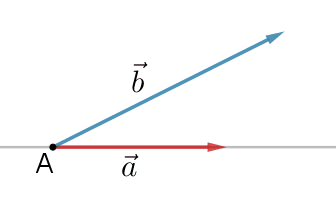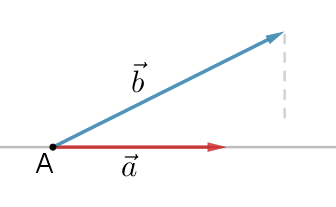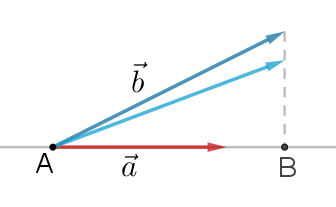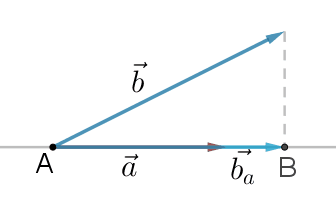
Vi projicerer $\vec{b}$ ’s endepunkt vinkelret ned på den linje, som indeholder $\vec{a}$ . Vi kalder dette punkt B. Projektionen af $\vec{b}$ på $\vec{a}$ er vektoren mellem A og B.

Projektionsvektoren noteres $\vec{b_a}$ . Da $\vec{b_a}$ ’s begyndelses- og endepunkt ligger på den linje, der indeholder $\vec{a}$ , så er $\vec{b_a}$ og $\vec{a}$ parallelle.

Bestem projektionsvektoren

Sætning. Projektionen af $\vec{b}$ på $\vec{a}$ .

Når $\vec{a}$ og $\vec{b}$ er egentlige vektorer, så er $\vec{b_a}$ projektionen af $\vec{b}$ på $\vec{a}$ . Projektionen er givet ved

$\vec{b_a} = \frac{\vec{a}\cdot\vec{b}}{|\vec{a}|^2} \cdot \vec{a}$

Vi beviser sætningen på siden Bevis for projektion af vektor på vektor.

Eksempel: Bestem projektionen af vektor b på vektor a

To vektorer $\vec{a}$ og $\vec{b}$ er givet ved

$\begin{align*} &\vec{a} = \binom{4}{2} \\[1em] &\vec{b} = \binom{2}{3} \end{align*}$

Vi vil bestemme projektionsvektoren $\vec{b_{a}}$ , dvs. projektionen af $\vec{b}$ på $\vec{a}$ .

Vi bestemmer først $\vec{a} \cdot \vec{b}$ og...

Teksten herover er et uddrag fra webbogen. Kun medlemmer kan læse hele indholdet.

Få adgang til hele Webbogen.

Som medlem på Studienet.dk får du adgang til alt indhold.

Køb medlemskab nu

Allerede medlem? Log ind