Koordinater til en vektor mellem to punkter

Forbindelsesvektor (vektor mellem to punkter)

Hvis vi kender to punkter A og B i planen, så kan vi forbinde dem med en vektor. Herunder har vi tegnet vektoren fra A til B:

En vektor, der er udspændt af to punkter, kaldes for en forbindelsesvektor. Forbindelsesvektorer navngives typisk efter de to punkter, som vektoren forbinder. Vektoren, der forbinder punkterne A og B på figuren herover, kalder vi , da den begynder i punkt A og ender i punkt B.

Notationen udtales "vektor AB", "vektoren fra A til B" eller "forbindelsesvektoren fra A til B".

Herunder kan du se fem eksempler på forbindelsesvektorer:

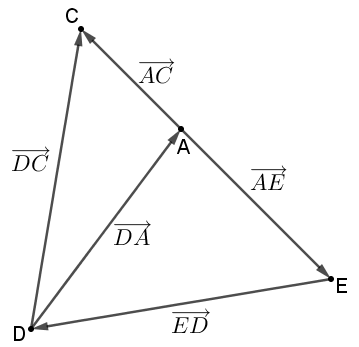
Bemærk, at det altid er begyndelsespunktet, der kommer først i en vektors navn. Den modsatte vektor til kaldes derfor typisk og ikke , da den modsatte vektor til er den vektor, der begynder i B og ender i A.

Selv om vi navngiver en vektor efter to punkter, så ændrer det ikke på, at vektoren har mere end én repræsentant. Vi ...