Vektorer i planen
  1. Vektorer i planen
[37]

Sum, differens og skalarmultiplikation

Indhold

Summen af to vektorer

Ligesom vi kan lægge tal sammen, så kan vi også lægge vektorer sammen. At lægge to vektorer sammen kaldes vektoraddition. Resultatet kaldes en vektorsum eller sumvektoren, da det er en vektor, der er summen af to andre vektorer.

Grafisk repræsentation af sumvektoren

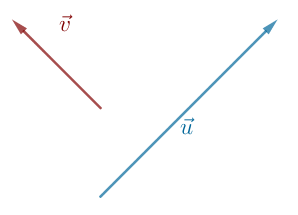
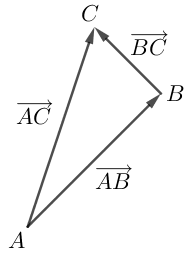
Herunder ses repræsentanter for to vektorer:

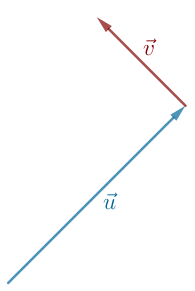
Hvis vi afsætter \vec{v} i \vec{u}'s endepunkt, så får vi:

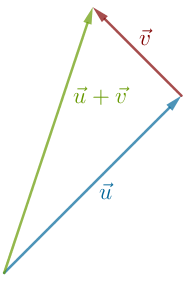
Summen af \vec{u} og \vec{v} er den vektor, der begynder i \vec{u}'s begyndelsespunkt og ender i \vec{v}'s endepunkt:

Du kan evt. tænke på vektorsummen som "den direkte vej" fra \vec{u}'s begyndelsespunkt til \vec{v}'s endepunkt eller resultatet af "først at følge \vec{u} og derefter \vec{v}".

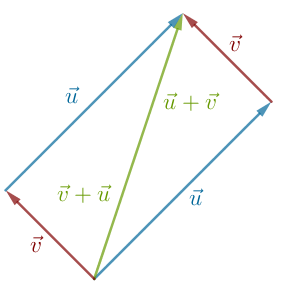
Hvis vi afsætter \vec{u} i \vec{v}'s endepunkt, så får vi samme resultat, som når vi afsætter \vec{v} i \vec{u}'s endepunkt:

Der gælder derfor, at

\vec{u} + \vec{v} = \vec{v} + \vec{u}

Rækkefølgen er altså ligegyldig, når vi lægger to vektorer sammen.

Indskudsreglen

Sætning. Indskudsreglen.

Når A, B og C er tre punkter i planen, så er

\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}

Vi kommer frem til indskudsreglen ved at bruge definitionen af summen af to vektor...

Teksten herover er et uddrag fra webbogen. Kun medlemmer kan læse hele indholdet.

Få adgang til hele Webbogen.

Som medlem på Studienet.dk får du adgang til alt indhold.

Køb medlemskab nu

Allerede medlem? Log ind

Notation og begreberRegneregler for vektorer