Arealet af en trekant udspændt af vektorer

Indhold

To vektorer udspænder en trekant
Determinanten benyttes til at bestemme trekantens areal
- Eksempel: Bestem arealet af trekanten udspændt af vektor a og vektor b
- Eksempel: Bestem arealet af trekant ABC
Opgaver om arealet af en trekant udspændt af to vektorer

To vektorer udspænder en trekant

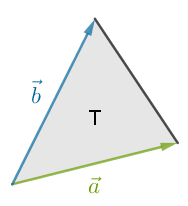
Når to egentlige vektorer afsættes i samme punkt, så kan vi danne en trekant ved at forbinde vektorernes endepunkter. Vi siger, at vektorerne udspænder trekanten.

Arealet af trekanten er halvt så stort som arealet af parallelogrammet udspændt af vektorerne:

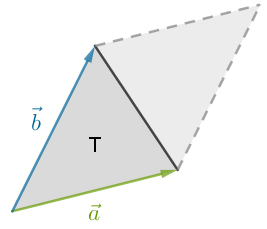
Determinanten benyttes til at bestemme trekantens areal

Sætning. Arealet af trekanten udspændt af to vektorer.

Hvis $\vec{a}$ og $\vec{b}$ er egentlige vektorer, og T er arealet af trekanten udspændt af $\vec{a}$ og $\vec{b}$ , så er

$T = \frac{1}{2} \cdot | \det ( \vec{a},\vec{b})|$

Tegnene | | har to betydninger: Hvis de står omkring en vektor, så er der tale om længden af vektoren; Hvis de står omkring et tal, så er der tale om den numeriske værdi af tallet. Determinanten mellem to vekto...

Teksten herover er et uddrag fra webbogen. Kun medlemmer kan læse hele indholdet.

Få adgang til hele Webbogen.

Som medlem på Studienet.dk får du adgang til alt indhold.

Køb medlemskab nu

Allerede medlem? Log ind