Parallelle vektorer

Ensrettede og modsatrettede vektorer

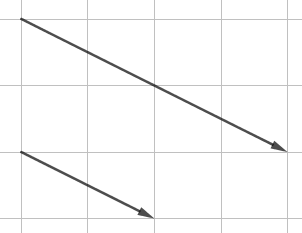
To vektorer kaldes ensrettede, hvis de har samme retning. På figuren herover kan du se to vektorer, der er ensrettede.

To vektorer kaldes modsatrettede, hvis de peger i modsat retning af hinanden. Figuren herover viser to modsatrettede vektorer.

En egentlig vektor, der har samme længde som en anden vektor , men modsat retning, kaldes den modsatte vektor til og betegnes typisk .

Parallelle vektorer er ens- eller modsatrettede

To vektorer er parallelle, hvis de er ensrettede eller modsatrettede. Det er ligegyldigt, hvor lange vektorerne er - det er kun retningen, der afgør, om vektorerne er parallelle. Figuren herover viser fire parallelle vektorer.

Hvis to vektorer er parallelle, så noterer vi det ved at benytte to parallelle streger:

Notationen betyder altså, at og er parallelle, dvs. at de er ensrettede eller modsatre...