Ortogonale vektorer

Indhold

To vektorer er ortogonale, når vinklen mellem dem er ret
Ortogonalitet og skalarprodukt
- Eksempel: Er vektor AB og vektor AC ortogonale?
- Eksempel: Bestem vektor a’s koordinater, så vektor a og vektor b er ortogonale
Opgaver om ortogonale vektorer

To vektorer er ortogonale, når vinklen mellem dem er ret

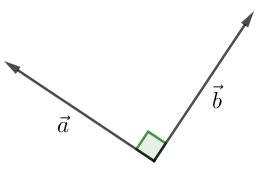
To vektorer i planen er ortogonale, når vinklen mellem dem er 90°, dvs. når vinklen er ret.

Symbolet $\perp$ bruges til at vise, at vektorer er ortogonale. Hvis vektorerne $\vec{a}$ og $\vec{b}$ er ortogonale, så skriver vi $\vec{a} \perp \vec{b}$ .

Ortogonalitet og skalarprodukt

Sætning. Ortogonale vektorer.

To egentlige vektorer $\vec{a}$ og $\vec{b}$ er ortogonale hvis og kun hvis

$\vec{a} \cdot \vec{b} = 0$

Vi beviser sætningen på siden Beviser med vinklen mellem to vektorer.

Eksempel: Er vektor AB og vektor AC ortogonale?

To vektorer er givet ved

$\begin{align*} \overrightarrow{AB} &= \binom{3}{5} \\[1em] \overrightarrow{AC} &= \binom{7}{-4} \end{align*}$

Vi vil undersøg...

Teksten herover er et uddrag fra webbogen. Kun medlemmer kan læse hele indholdet.

Få adgang til hele Webbogen.

Som medlem på Studienet.dk får du adgang til alt indhold.

Køb medlemskab nu

Allerede medlem? Log ind