Retningsvinkel
Hvad er retningsvinklen?
En enhedsvektor har længden 1, så hvis vi afsætter en enhedsvektor 
Vinklen v mellem den positive del af førsteaksen og enhedsvektoren i positiv omløbsretning (dvs. mod uret) kalder vi for vektorens retningsvinkel. Endepunktet Pv kalder vi for retningspunktet for v.
Der findes en enhedsvektor i enhver retning, dvs. at til enhver egentlig vektor 




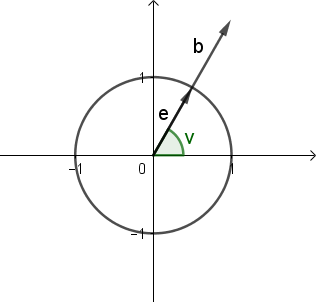
Cosinus og sinus
.png)
R...

