Hvad er en vektorfunktion?
Definition af vektorfunktion
Herunder er et eksempel på en vektorfunktion:
Til enhver værdi af t knytter vektorfunktionen 

Hvis fx t = 2, så er
Vektorfunktionen 

Vi noterer en vektorfunktion med et bogstav med en pil over, ofte 


Eksempel
Herunder ses tre eksempler på vektorfunktioner:
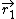 er defineret på intervallet I =
er defineret på intervallet I = 


Koordinatfunktioner
En vektorfunktion er på formen
x(t) og y(t) er funktioner defineret på I...


![\begin{align*} \vec{r}(2) &= \binom{2}{2^2} \\[1em] &= \binom{2}{4} \end{align}](/media/webbooks/preview/2199/30722/images/equations/dowfm8dgmiytl2vdwirzxg==.svg)
![\begin{align*} \vec{r_1}(t) &= \binom{3}{-t}, \quad t \in \mathbb{R} \\[1em] \vec{r_2}(t) &= \binom{2 + \sin(t)}{\cos(3t)}, \quad t \in [0;2\pi[ \\[1em] \vec{r_3}(t) &= \binom{\sqrt{t}}{2 + t}, \quad t \in [0;\infty[ \end{align}](/media/webbooks/preview/2199/30722/images/equations/w21mrclio_g6i9kee3db5g==.svg)

