Uden hjælpemidler
Her finder du facit og vores løsninger til opgaverne i prøven uden hjælpemidler fra Matematik FP9 4. december 2018.
Du kan få hjælp til at løse en lang række af opgaverne i vores vejledning til FP9 færdighedsregning.
Opgave 1
1.1
Hvor mange penge koster den blå hjelm mere end den røde hjelm?
350 kr.
Træk prisen for den røde hjelm (449 kr.) fra prisen for den blå hjelm (799 kr.).
Vi beregner, hvor meget den blå hjelm koster mere end den røde hjelm ved at trække prisen for den røde hjelm fra prisen for den blå hjelm:
Den blå hjelm koster 350 kr. mere end den røde hjelm.
1.2
Hvor mange penge koster den røde hjelm og tasken i alt?
698 kr.
Læg prisen for den røde hjelm (449 kr.) sammen med prisen for tasken (249 kr.).
Vi beregner prisen for den røde hjelm og tasken ved at lægge priserne for de to ting sammen:
Den røde hjelm og tasken koster 698 kr. i alt.
1.3
Hvor mange penge kan Gustav få i rabat på ishockeystaven?
Du kan se flere opgaver af den her type, og hvordan vi løser dem, i vores vejledning til opgaver om procent.
34,90 kr.
At gange med 0,10 er det samme som at dele med 10.
Vi beregner Gustavs rabat på ishockeystaven ved at beregne 10% af 349 kr.
Da 10% = 0,10, så kan vi beregne 10% af 349 kr. ved at gange 349 med 0,10. At gange med 0,10 svarer til at dele med 10. Det er nemmere at dele med 10, så vi deler 349 kr. med 10. Vi deler med 10 ved at rykke kommaet én plads mod venstre:
349 : 10 = 34,9
Gustav kan få 34,90 kr. i rabat.
Opgave 2
2.1
Hvor mange minutter skal en skinke på 1,5 kg koge?
60 minutter
Vi får oplyst, at en skinke skal koge 40 min. pr. kg, dvs. at en skinke på 1 kg skal koge i 40 min., og en skinke på 1,5 kg skal koge 1,5 gang så lang tid.
Vi får oplyst, at en skinke skal koge 40 min. pr. kg, dvs. at en skinke på 1 kg skal koge i 40 min., og en skinke på 1,5 kg skal koge 1,5 gang så lang tid:
| Vægt (kg) | Kogetid (min.) |
| 1 | 40 |
| 0,5 | 20 |
| 1,5 | 60 |
En skinke på 1,5 kg skal koge i 60 min.
2.2
Hvor mange minutter skal en skinke på 0,8 kg koge?
32 minutter
Beregn først, hvor lang tid en skinke på 0,1 kg skal koge.
Vi får oplyst, at en skinke skal koge 40 min. pr. kg, dvs. at en skinke på 1 kg skal koge i 40 min., og en skinke på 0,1 kg skal koge 1/10 så lang tid:
| Vægt (kg) | Kogetid (min.) |
| 1 | 40 |
| 0,1 | 4 |
| 0,2 | 8 |
| 0,4 | 16 |
| 0,8 | 32 |
En skinke på 0,8 kg skal koge i 32 min.
Opgave 3
3.1
Hvor mange gram kød skal Gustav bruge til 7 personer?
875 g
Gang mængden af kød pr. person (125 g) med antallet af personer (7).
Vi beregner, hvor meget kød Gustav skal bruge til 7 personer, når han skal bruge 125 g pr. person:
Gustav skal bruge 875 g kød pr. person.
3.2
Hvad er det højeste antal personer, der kan få 75 g spaghetti hver, hvis Gustav har 500 g spaghetti?
6 personer
Del 500 med 75, eller undersøg, hvor meget spaghetti der skal bruges til forskellige antal personer.
Vi beregner, hvor meget spaghetti der skal bruges til forskellige antal personer:
| Antal personer | Spaghetti (g) |
| 1 | 75 |
| 2 | 150 |
| 4 | 300 |
| 6 | 450 |
| 7 | 525 |
6 personer kan få 75 g spaghetti hver.
Opgave 4
4.1
Hvad er det mindste antal flasker, hun kan have fået pant for?
6
Jo flere store flasker Rikke har fået pant for, jo færre flasker har hun fået pant for.
Store flasker giver mere i pant, så jo flere store flasker Rikke har fået pant for, jo færre flasker har hun fået pant for.
Hvis Rikke har fået pant for 5 store flasker, så har hun fået 15 kr.i pant. Hun kan ikke have pantet 6 store flasker, da hun så ville have fået 18 kr. i pant.
Rikke har fået 16 kr. i pant, så hun må have pantet 5 store flasker og 1 lille flaske, dvs. 6 flasker i alt.
4.2
Hvor mange små flasker har Gustav fået pant for?
4
Udfyld et skema som herunder. Husk, at Gustav har pantet 10 flasker i alt.
| Antal store flasker | Antal små flasker | Pant |
| 1 | ||
| 2 | ||
| 3 | ||
Vi prøver os frem med forskellige antal store flasker. Da Gustav har pantet 10 flasker, så kan vi efterfølgende regne os frem til, hvor mange små flasker, han har pantet, og dermed hvad han har fået i pant:
| Antal store flasker | Antal små flasker | Pant |
| 1 | 9 | 1 · 3 + 9 · 1 = 12 |
| 2 | 8 | 2 · 3 + 8 · 1 = 14 |
| 3 | 7 | 3 · 3 + 7 · 1 = 16 |
| 4 | 6 | 4 · 3 + 6 · 1 = 18 |
| 5 | 5 | 5 · 3 + 5 · 1 = 20 |
| 6 | 4 | 6 · 3 + 4 · 1 = 22 |
Gustav har fået pant for 4 små flasker.
Opgave 5
5.1
Regn 1251 + 351.
1602
5.2
Regn 904 – 849.
55
5.3
Regn 6 · 806.
4836
5.4
Regn 3556 : 7.
508

Opgave 6
6.1
Skriv som heltal:
70
1/3 af 21 er 7.
1/3 af 21 er 7, fordi 7 + 7 + 7 = 21.
Da 210 er 10 gange større end 21, så er 1/3 af 210 også 10 gange større end 1/3 af 21. 1/3 af 210 er dermed 70 (dvs. 10 · 7).
6.2
Skriv som heltal:
3,5 · 106
3500000
Da 106 = 10 · 10 · 10 · 10 · 10 · 10, så er
3,5 · 106 = 3,5 · 10 · 10 · 10 · 10 · 10 · 10
Vi ganger et tal med 10 ved at rykke kommaet én plads mod højre. Vi ganger derfor 6 gange med 10 ved at rykke kommaet seks pladser mod højre:
3,5000000 · 10 · 10 · 10 · 10 · 10 · 10 = 3500000,0
6.3
Skriv som heltal:
2
Start med at gange 2 og 4 i tælleren og forkort derefter brøken.
Vi ganger 2 og 4 i tælleren:
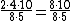
Vi forkorter brøken med 8:
Vi forkorter brøken med 5:
6.4
Skriv som heltal:
10 - 2 · 6
-2
Resultatet er negativt.
Vi omskriver udtrykket:
Opgave 7
7.1
Løs ligningen 4x – 7 = 13.
Du kan se flere opgaver af den her type, og hvordan vi løser dem, i vores vejledning til opgaver om ligninger.
x = 5
Isolér x ved at lægge 7 til på begge sider af lighedstegnet og derefter dele med 4.
Vi opskriver ligningen:
Vi lægger 7 til på begge sider af lighedstegnet:
Vi får så:
Vi deler med 4 på begge sider af lighedstegnet:
Vi får så:
7.2
Løs ligningen 5x + 10 = 18 + x.
Du kan se flere opgaver af den her type, og hvordan vi løser dem, i vores vejledning til opgaver om ligninger.
x = 2
Isolér x. Træk først x fra på begge sider af lighedstegnet og træk derefter 10 fra.
Vi opskriver ligningen:
Vi trækker x fra på begge sider af lighedstegnet:
Vi får så:
Vi trækker 10 fra på begge sider af lighedstegnet:
Vi får så:
Vi deler med 4 på begge sider af lighedstegnet:
Vi får så:
7.3
Løs ligningen
Du kan se flere opgaver af den her type, og hvordan vi løser dem, i vores vejledning til opgaver om ligninger.
x = -1
Isolér x. Gang først med 2 på begge sider af lighedstegnet for at "slippe af med" brøkerne.
Vi opskriver ligningen:
Vi ganger med 2 på begge sider af lighedstegnet:
Vi ganger 2 ind i hver parentes ved at gange hvert led med 2:
Vi får så:
Vi trækker x fra på begge sider af lighedstegnet:
Vi får så:
Vi trækker 2 fra på begge sider af lighedstegnet:
Vi får så:
Opgave 8
8.1
Indsæt et tal, så udtrykket bliver sandt:
4 + 8 = ___ + 5
7
Beregn først 4 + 8.
Vi opskriver udtrykket:
4 + 8 = ___ + 5
Vi beregner 4 + 8:
12 = ___ + 5
Opgaven svarer altså til at finde ud af, hvad vi skal lægge til 5 for at få 12. Vi skal lægge 7 til 5 for at få 12.
8.2
Indsæt et tal, så udtrykket bliver sandt:
16 · 100 = ____ · 200
x = 8
16 er 8 gange større end 2.
Vi opskriver udtrykket:
16 · 100 = ____ · 200
Vi beregner 16 · 100:
1600 = ____ · 200
Da 16 er 8 gange større end 2, så er 1600 også 8 gange større end 200:
1600 = 8 · 200
8.3
Indsæt et tal, så udtrykket bliver sandt:
(0,3 eller en brøk, der kan forkortes til 3/10, er også et korrekt facit.)
Forlæng begge brøker, så de får nævneren 10.
Vi opskriver udtrykket:
Vi forlænger brøken på venstre side af lighedstegnet med 5, så den får 10 i nævneren:
Vi forlænger derefter brøken på højre side af lighedstegnet med 2, så den også får 10 i nævneren:
Vi skal lægge 3/10 til 2/10 for at få 5/10:
Opgave 9
9.1
Hvilken værdi har f(x), når x = 5?
7
Undersøg, hvor meget funktionsværdien vokser, når x vokser med 1.
Vi kan se i tabellen, at når værdien af x vokser med 1, så vokser funktionsværdien f(x) også med 1. Vi udvider tabellen:
| x | f(x) |
| 0 | 2 |
| 1 | 3 |
| 2 | 4 |
| 3 | 5 |
| 4 | 6 |
| 5 | 7 |
Når x = 5, så har f(x) værdien 7.
9.2
Skriv en forskrift for funktionen f.
x + 2
Vi får funktionsværdien ved at lægge 2 til x-værdien.
Vi kan se, at vi får funktionsværdien ved at lægge 2 til x-værdien:
| x | f(x) |
| 0 | 2 (= 0 + 2) |
| 1 | 3 (= 1 + 2) |
| 2 | 4 (= 2 + 2) |
| 3 | 5 (= 3 + 2) |
| 4 | 6 (= 4 + 2) |
Funktionen er derfor givet ved forskriften
f(x) = x + 2
Opgave 10
10.1
Omkredsen af den blå figur er?
2a + 2b + 10
Beregn omkredsen ved at lægge længderne af alle fire sider sammen.
Vi får oplyst, at et rektangel har sidelængderne 2 + a og 3 + b. Vi beregner omkredsen ved at lægge længderne af alle fire sider sammen:
2 + a + 3 + b + 2 + a + 3 + b = 2a + 2b + 10
Omkredsen er 2a + 2b + 10.
10.2
Arealet af den blå figur er?
ab + 3a + 2b + 6
Opdel det blå rektangel i fire mindre rektangler, og bestem arealet af hvert af de fire rektangler.
Det blå rektangel består af fire mindre rektangler (I, II, III og IV):

Vi beregner arealet af hvert rektangel ved at gange længden og bredden:
| Rektangel | Længde | Bredde | Areal |
| I | b | a | b · a = ab |
| II | 3 | a | 3 · a = 3a |
| III | b | 2 | b · 2 = 2b |
| IV | 3 | 2 | 3 · 2 = 6 |
Da det blå rektangel kan opdeles i de fire mindre rektangler, så kan vi bestemme arealet af det blå rektangel ved at lægge arealerne af de fire mindre rektangler sammen.
Arealet af det blå rektangel er
ab + 3a + 2b + 6
Opgave 11
11.1
Hvor stort er arealet af et trapez, hvor højden h er 3, sidelængden a er 2, og sidelængden b er 4?
9
Sæt h = 3, a = 2 og b = 4 ind i formlen i den gule boks.
Vi beregner arealet ved at sætte højden h = 3, sidelængden a = 2 og sidelængden b = 4 ind i formlen i den gule boks:
 | = |  |
| = |  | |
| = |  | |
| = |  |
Arealet af trapezet er 9.
11.2
Hvor stor er højden h i et trapez, hvor arealet er 35, sidelængden a er 4, og sidelængden b er 10?
5
Sæt arealet A = 35, sidelængden a = 4 og sidelængden b = 10 ind i formlen i den gule boks og isolér højden h.
Vi sætter arealet A = 35, sidelængden a = 4 og sidelængden b = 10 ind i formlen i den gule boks:
Vi har nu en ligning, som vi kan løse. Vi beregner først, at 4 + 10 = 14, dvs. at
Vi beregner derefter, at 14/2 = 7, dvs. at
Vi deler nu med 7 på begge sider af lighedstegnet:
Vi får så, at
Højden h er 5.
Opgave 12
12.1
Førstekoordinaten til punktet A er?
-2
Vi aflæser førstekoordinaten til punkt A på x-aksen.
Vi aflæser førstekoordinaten til punkt A på x-aksen:

12.2
Arealet af trekant ABC er?
9
Opdel trekanten i mindre trekanter:

Vi opdeler trekant ABC i tre mindre trekanter (I, II og III):

Kateterne i trekant I har længden ½ og 2, så trekant I og III udgør tilsammen en retvinklet trekant:

Vi kan se på figuren, at trekant II har en grundlinje med længden 4, og at den tilhørende højde er 2. Arealet af trekant II er derfor
Trekant III og I udgør en retvinklet trekant, hvor en af grundlinjerne har længden 5, og den tilhørende højde er 2. Arealet af trekant I og III tilsammen er derfor
Vi bestemmer arealet af trekant I, II og III tilsammen:
Arealet af trekant ABC er 9.
Opgave 13
13.1
Omskriv 400 m.
Du kan se flere opgaver af den her type, og hvordan vi løser dem, i vores vejledning til opgaver om omregning af enheder.
0,4 km
1000 m er 1 km.
Der går 1000 m på 1 km, så vi omskriver 400 m til km ved at dele 400 med 1000:
400 : 1000 = 0,4
400 m er 0,4 km.
13.2
Omskriv 
210
1 time er 60 minutter.
Der går 60 minutter på 1 time:
| Timer | Minutter |
| 1 | 60 |
| 0,5 | 30 |
| 2 | 120 |
| 3 | 180 |
| 3,5 | 210 |
3½ time er 210 minutter.
13.3
Omskriv 205 g.
Du kan se flere opgaver af den her type, og hvordan vi løser dem, i vores vejledning til opgaver om omregning af enheder.
0,205
1000 g er 1 kg.
Der går 1000 g på 1 kg, så vi omskriver 205 g til kg ved at dele 205 med 1000:
205 : 1000 = 0,205
205 g er 0,205 kg.
13.4
Omskriv 150 ml.
Du kan se flere opgaver af den her type, og hvordan vi løser dem, i vores vejledning til opgaver om omregning af enheder.
1,5
100 ml er 1 dl.
Der går 100 mL på 1 dl, så vi omskriver 150 ml til dl ved at dele 150 med 100:
150 : 100 = 1,5
150 ml er 1,5 dl.
Opgave 14
14.1
Hvor lang er siden d i trekant DEF, hvis siden a i trekant ABC er 5?
Du kan se flere opgaver af den her type, og hvordan vi løser dem, i vores vejledning til opgaver om ligedannede figurer.
15
Længdeforholdet mellem de to ligedannede trekanter er 1:3, dvs. at siderne i trekant DEF er 3 gange så lange som de tilsvarende sider i trekant ABC.
Vi får oplyst, at længdeforholdet mellem de to ligedannede trekanter er 1:3, dvs. at siderne i trekant DEF er 3 gange så lange som de tilsvarende sider i trekant ABC.
Hvis siden a i trekant ABC er 5, så er siden d i trekant DEF derfor 3 gange så lang, dvs. at længden af siden d er 15.
14.2
Hvor stor er vinkel A i trekant ABC, hvis vinkel E i trekant DEF er 30°?
60°
Da trekant ABC og trekant DEF er ligedannede, så er vinklerne i trekanterne parvist lige store.
Da trekant ABC og trekant DEF er ligedannede, så er vinklerne i trekanterne parvist lige store:
Vinkel A og vinkel D er lige store.
Vinkel B og vinkel E er lige store.
Vinkel C og vinkel F er lige store.
Da vinkel A er 30°, så er vinkel D derfor også 30°.
Da vinkel D er 30°, og vinkel F er ret (dvs. 90°), så kan vi bestemme vinkel E ud fra vinkelsummen i en trekant (180°):
30° + 90° + E = 180°
Vi trækker 90° fra på begge sider af lighedstegnet:
30° + E = 90°
Vi trækker 30° fra på begge sider af lighedstegnet:
E = 60°
Vinkel E er 60°.
14.3
Hvor stort er arealet af trekant DEF, hvis arealet af trekant ABC er 10?
Du kan se flere opgaver af den her type, og hvordan vi løser dem, i vores vejledning til opgaver om ligedannede figurer.
90
Undersøg, hvor mange kopier af den lille trekant, der kan placeres i den store trekant.
Siderne i den store trekant DEF er 3 gange så lange, som siderne i den lille trekant ABC. Vi kan derfor placere 3 kopier af den lille trekant ved siden af hinanden langs siderne i den store trekant:

Arealet af den store trekant DEF er 9 gange så stort som arealet af den lille trekant ABC.
Hvis trekant ABC har arealet 10, så har trekant DEF derfor arealet 90.
Opgave 15
15.1
Hvilken af trekanterne er ligesidet?
A
En trekant er ligesidet, hvis alle tre sider er lige lange.
15.2
Hvilken af trekanterne er spidsvinklet?
A
En trekant er spidsvinklet, hvis alle tre vinkler er spidse.
Trekant A har 3 spidse vinkler, så trekant A er spidsvinklet.
Opgave 16
16.1
Kassens rumfang er?
Du kan se flere opgaver af den her type, og hvordan vi løser dem, i vores vejledning til opgaver om rumfang og overfladeareal af prismer.
500
Rumfanget kan bestemmes ved at gange arealet af grundfladen med højden.
Vi bestemmer rumfanget ved at gange arealet af grundfladen med højden. Højden er 5.
Vi får oplyst, at den kvadratiske grundflade har sidelængden 10. Vi bestemmer arealet, G, af grundfladen:
Grundfladen har et areal på 100.
Vi bestemmer rumfanget:
Rumfanget er 500.
16.2
Kassens samlede overfladeareal er?
Du kan se flere opgaver af den her type, og hvordan vi løser dem, i vores vejledning til opgaver om rumfang og overfladeareal af prismer.
400
Figuren har seks sider. Bestem arealet af hver side, og læg arealerne sammen.
Vi bestemmer overfladearealet ved at bestemme arealet af hver side og lægge alle arealerne sammen.
Kassen har seks sider. To af siderne er identiske kvadratiske sider med sidelængden 10. De fire andre sider er identiske rektangulære sider med længden 10 og bredden 5.
Vi bestemte i opg. 16.1, at de kvadratiske sider har et areal på 100. Vi bestemmer arealet af hver af de rektangulære sider:
Hver af de rektangulære sider har et areal på 50.
Vi bestemmer kassens overfladeareal:
Overfladearealet er 400.
Opgave 17
17.1
Hvilket rosettemønster har drejningssymmetri, men ikke spejlingssymmetri?
D
Alle mønstrene har drejningssymmetri. Undersøg, hvilken figur der ikke har spejlingssymmetri.

Hvis vi roterer rosettemønster D omkring midtpunktet, så kan vi føre mønsteret "over i sig selv", dvs. at mønsteret har drejningssymmetri.
Vi kan ikke tegne en linje gennem rosettemønster D, så mønsteret på den ene side af linjen er en spejling af mønsteret på den anden side af linjen, så mønsteret har ikke spejlingssymmetri.
For de fire andre mønstre gælder der, at vi kan tegne en linje gennem mønsteret, så mønsteret på den ene side af linjen er en spejling af mønstret på den anden side af linjen.
17.2
Hvilket rosettemønster har netop 4 symmetriakser?
B
Rosettemønster D har ikke spejlingssymmetri.
Tegn symmetriakser på de andre figurer. Her er et eksempel på en symmetriakse:

Rosettemønster D har ikke spejlingssymmetri.
Vi tegner symmetriakser på de andre figurer:

Figur B har netop 4 symmetriakser. De andre figurer har ingen (D) eller færre end 4 symmetriakser (A, B og E).
Opgave 18
18.1
Hvilket af udsagnene er sandt?
Mere end halvdelen af eleverne i 9. B har fået karakteren 4 eller derunder.
Undersøg hvert udsagn.
Du kan aflæse elevernes karakterer på diagrammet. På den vandrette akse ses de forskellige karakterer. Antallet af elever, der har fået hver karakter, kan aflæses på den lodrette akse.
| Udsagn | Sandt? | Forklaring |
|---|---|---|
| Der er fire elever i 9. B, der har fået karakteren 12. | Nej | Der er 2 elever i 9. B, der har fået karakteren 12. |
| Der er flere elever i 9. B end i 9. A. | Nej | Der er 25 elever i 9. A og 23 elever i 9. B. |
| Der er givet flest forskellige karakterer i 9. B. | Nej | I 9. A er der givet 7 forskellige karakterer (-2, 00, 02, 4, 7, 10 og 12). I 9. B er der givet 5 forskellige karakterer (02, 4, 7, 10 og 12). |
| Mere end halvdelen af eleverne i 9. B har fået karakteren 4 eller derunder. | Ja | Der er 13 elever, der har fået karakteren 4 eller derunder, og 10 elever, der har fået karakterer over 4. |
| Det højeste antal elever i 9. B, der har fået samme karakter, er fire. | Nej | Der er fx 8 elever, der har fået karakteren 4. |
Opgave 19
19.1
Cirka hvor mange penge brugte husstande i Region Sjælland?
190
(Det kan være lidt svært at aflæse præcist i diagrammet, så svar mellem 185 og 195 er også korrekte.)
Undersøg, hvor mange penge hvert julehjerte svarer til i diagrammet, når Region Nordjylland har 6,5 julehjerter, og husstande i Region Nordjylland brugte ca. 130 kr.
Vi får oplyst, at husstande i Region Nordjylland brugte ca. 130 kr. på julepynt og fyrværkeri. Vi aflæser, at der er 6,5 julehjerte ud for Region Nordjylland i diagrammet.
Da 2 · 6,5 = 13, så er 20 · 6,5 = 130. Hvert julehjerte svarer altså ca. til 20 kr.
Vi aflæser, at der er 9,5 julehjerter ud for Region Sjælland. Vi beregner, hvor mange penge 9,5 julehjerter svarer til, når hvert julehjerte er 20 kr.:
| Antal julehjerter | Antal kroner |
| 1 | 20 |
| 0,5 | 10 |
| 2 | 40 |
| 4 | 80 |
| 8 | 160 |
| 9 | 180 |
| 9,5 | 190 |
Husstande i Region Sjælland brugte ca. 190 kr.
19.2
Cirka hvor mange procent brugte hustande i Region Midtjylland mindre
end husstande i Region Hovedstaden?
50%
(Det kan være lidt svært at aflæse præcist i diagrammet, så svar mellem 45% og 55% er også korrekte.)
Undersøg, hvor mange procent færre hjerter der er ud for Region Midtjylland end ud for Region Hovedstaden. Du behøver altså ikke at regne ud, hvor mange penge husstandene i de to regioner brugte.
Vi aflæser, at der er ca. 5 julehjerter ud for Region Midtjylland, og at der er ca. 10 julehjerter ud for Region Hovedstaden. Husstande i Region Midtjylland brugte altså ca. halvt så mange penge, som husstande i Region Hovedstaden, dvs. at de brugte 50% mindre.
Opgave 20
20.1
Hvor stor er sandsynligheden for, at Gustav trækker et es?
1/10
(10% eller 0,1 eller en brøk, der kan forkortes til 1/10, er også korrekte svar.)
Du kan bestemme sandsynligheden for hændelsen H med formlen
Der er 1 es blandt 10 kort:
Sandsynligheden for at Gustav trækker et es, er 1/10.
20.2
Hvor stor er sandsynligheden for, at Gustav ikke trækker en konge?
7/10
(70% eller 0,7 eller en brøk, der kan forkortes til 7/10, er også korrekte svar.)
Du kan bestemme sandsynligheden for hændelsen H med formlen
Der er 3 konger, dvs. at der er 7 kort, der ikke er konger:
Sandsynligheden for at Gustav ikke trækker en konge, er 7/10.
20.3
Hvor stor er sandsynligheden for, at Gustav trækker enten en konge eller en dame?
1/2
(50% eller 0,5 eller en brøk, der kan forkortes til 1/2, er også korrekte svar.)
Du kan bestemme sandsynligheden for hændelsen H med formlen
Der er 3 konger og 2 damer, dvs. at der er 5 kort med en konge eller dame:
Sandsynligheden for at Gustav trækker en konge eller en dame, er 1/2.













![\begin{align*} 10 - 2 \cdot 6 &= 10 - 12 \\[1em] &= -2 \end{align}](https://media.studienet.dk/files/webbooks/images/3880/equations/TrPhxkQ4oW-QPUxchF-mKg==.svg)































![\begin{align*} T_{\text{II}} &= \frac{1}{2} \cdot 2 \cdot 4 \\[1em] &= 4 \end{align}](https://media.studienet.dk/files/webbooks/images/3880/equations/HkpbvKBMNONQEGXCcviRwg==.svg)
![\begin{align*} T_{\text{I + III}} &= \frac{1}{2} \cdot 2 \cdot 5 \\[1em] &= 5 \end{align}](https://media.studienet.dk/files/webbooks/images/3880/equations/5e-xy-PtO01sfGaGI0_D8A==.svg)
![\begin{align*} T_{\text{II}} + T_{\text{I + III}} &= 4 + 5 \\[1em] &= 9 \end{align}](https://media.studienet.dk/files/webbooks/images/3880/equations/G9ZZ_m4XEbxgPwfqO3Z_QA==.svg)
![\begin{align*} G &= 10 \cdot 10 \\[1em] &= 100 \end{align}](https://media.studienet.dk/files/webbooks/images/3880/equations/S-duggdOVs46FFq2YFwqrg==.svg)
![\begin{align*} V &= G \cdot h \\[1em] &= 100 \cdot 5 \\[1em] &= 500 \end{align}](https://media.studienet.dk/files/webbooks/images/3880/equations/VB9bJnIj95AGL5gsw0AaAQ==.svg)
![\begin{align*} A_{\text{rektangul\ae r}} &= 10 \cdot 5 \\[1em] &= 50 \end{}](https://media.studienet.dk/files/webbooks/images/3880/equations/taQTLxNxsjGFTy2KPxU1bQ==.svg)
![\begin{align*} 2 \cdot 100 + 4 \cdot 50 &= 200 + 200 \\[1em] &= 400 \end{align}](https://media.studienet.dk/files/webbooks/images/3880/equations/iA9bOxv_ReP6XngdYuKcMg==.svg)

![\begin{align*} P(\text{es}) &= \frac{\text{antal esser}}{\text{antal kort i alt}} \\[1em] &= \frac{1}{10} \end{align}](https://media.studienet.dk/files/webbooks/images/3880/equations/cLBXFzDCXyY1jCTbOMtXSw==.svg)
![\begin{align*} P(\text{ikke konge}) &= \frac{\text{antal kort, der ikke er konger}}{\text{antal kort i alt}} \\[1em] &= \frac{7}{10} \end{align}](https://media.studienet.dk/files/webbooks/images/3880/equations/eal3GPJ3VRw-eU26VHPImw==.svg)
![\begin{align*} P(\text{konge eller dame}) &= \frac{\text{antal konger og damer}}{\text{antal kort i alt}} \\[1em] &= \frac{5}{10} \\[1em] &= \frac{1}{2} \end{align}](https://media.studienet.dk/files/webbooks/images/3880/equations/VfgpFbXIs_VYe_BWL8Qs8Q==.svg)