Beviser med modulus og argument

Indhold

Produktet af z og den komplekst konjugerede til z

Sætning. Produktet af z og $\bar{z}$ .

Når z ∈ $\mathbb{C}$ , så er

$z \cdot \bar{z} = |z|^{2}$

Du kan se et eksempel, hvor vi bruger ovenstående sætning, på siden Modulus og argument.

Vi lader $z \in \mathbb{C}$ , dvs. at der findes to reelle tal a og b, så

z = a + bi

Den komplekst konjugerede til z er dermed

$\bar{z} = a - bi$

Vi bestemmer produktet af z og den komplekst konjugerede til z ved at indsætte z = a + bi og $\bar{z}$ = a - bi:

Herover har vi vist, at $z \cdot \bar{z}$ = a2 + b2.

Derefter bestemmer vi |z|2:

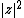Herover har vi vist, at |z|2 = a2 + b2.

Vi bemærker, at

$z \cdot \bar{z} = a^2 + b^2 = |z|^{2}$

Vi har altså vist, at

$z \cdot \bar{z} = |z|^{2}$

$\square$

Sætning. Modulus og argument for $\bf{\bar{z}}$ .

Når z ∈ $\mathbb{C}$ , så er

$|\bar{z}| = |z|$

$\arg(\bar{z}) = -\arg(z)$

Du kan se et eksempel, hvor vi bruger ovenstående sætning, på siden Modulus og argument.

Vi lader $z \in \mathbb{C}$ . De...

	=	$\left ( \sqrt{a^2 + b^2} \right )^2$
	=