Linjer, planer, afstand, skæring, vinkler og projektion

Linjer

Retningsvektor

En vektor, der er parallel med en linje, kaldes en retningsvektor for linjen.
Der findes uendeligt mange vektorer, der er parallelle med en given linje. Enhver linje har altså uendeligt mange retningsvektorer.

Parameterfremstilling

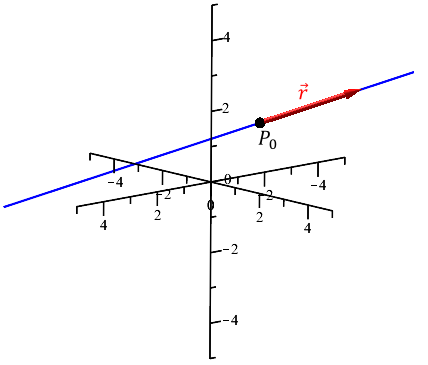
Linjen, der går gennem punktet P0(x0,y0,z0) og har retningsvektoren

$\vec{r} = \begin{pmatrix} r_1\\ r_2\\ r_3 \end{pmatrix}$

$\begin{pmatrix} x\\ y\\ z \end{pmatrix} = \begin{pmatrix} x_0\\ y_0\\ z_0 \end{pmatrix} + t \cdot \begin{pmatrix} r_1\\ r_2\\ r_3 \end{pmatrix}, \quad t \in \mathbb{R}$

Eksempel: Linjen l, der går gennem punktet P(1,0,-2) og har retningsvektoren $\vec{r} = \begin{pmatrix} 2\\ 2\\ -1 \end{pmatrix}$ er givet ved parameterfremstillingen

$\begin{pmatrix} x\\ y\\ z \end{pmatrix} = \begin{pmatrix} 1\\ 0\\ -2 \end{pmatrix} + t \cdot \begin{pmatrix} 2\\ 2\\ -1 \end{pmatrix}, \quad t \in \mathbb{R}$

Den variable i en parameterfremstilling kaldes parameteren. Vi benytter typisk t som parameter, men vi kan også vælge fx s .
En linje har uendeligt mange parameterfremstillinger.
To linjer i rummet er parallelle, hvis linjernes retningsvektorer er parallelle.
Få hjælp til at løse opgaver, hvor du skal bestemme en parameterfremstilling for en linje, i vejledningen Bestem en parameterfremstilling for en linje.

Vindskæve linjer

To linjer i rummet, som ikke er parallelle, men som heller ikke skærer hinanden, kaldes vindskæve.
Når to linjer er vindskæve, så ligger de i to parallelle planer. Her er et eksempel:

Planer

Hvad er en plan?

En plan er et fladt to-dimensionelt objekt i rummet.
Planer navngives ofte med græske bogstaver, fx α eller β.
En plan kan defineres ud fra tre forskellige punkter (der ikke ligger på linje). En plan kan også defineres ud fra et punkt og to vektorer. Vi siger i så fald, at vektorerne udspænder planen.

Parameterfremstilling

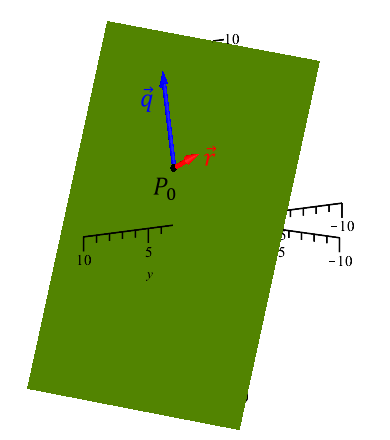
Planen, der indeholder punktet P0(x0,y0,z0) og er udspændt af to ikke-parallelle vektorer

$\begin{align*} \vec{r} &= \begin{pmatrix} r_1 \\ r_2 \\ r_3 \end{pmatrix} \\[1em] \vec{q} &= \begin{pmatrix} q_1 \\ q_2 \\ q_3 \end{pmatrix}, \end{align}$

er givet ved parameterfremstillingen

$\begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} + t \cdot \begin{pmatrix} r_1 \\ r_2 \\ r_3 \end{pmatrix} + s \cdot \begin{pmatrix} q_1 \\ q_2 \\ q_3 \end{pmatrix}, \quad s, t \in \mathbb{R}$

s og t er parametre.

Eksempel: Planen α indeholder punktet P0(1,2,3) og er udspændt af to ikke-parallelle vektorer $\vec{r} = \begin{pmatrix} -2 \\ 0 \\ 1 \end{pmatrix}$ og $\vec{q} = \begin{pmatrix} 3 \\ -2 \\ 5 \end{pmatrix}$ . Planen α er derfor givet ved parameterfremstillingen

$\begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + t \cdot \begin{pmatrix} -2 \\ 0 \\ 1 \end{pmatrix} + s \cdot \begin{pmatrix} 3 \\ -2 \\ 5 \end{pmatrix}, \quad s, t \in \mathbb{R}$

Til ethvert par af værdier (s0 og t0) af parametrene s og t i en parameterfremstilling hø

...