December 2021
Her er vores besvarelse til Matematik FP10 fra 3. december 2021.
Besvarelsen indeholder opgavernes facit og vores løsninger. Besvarelsen indeholder også hints, som du kan bruge, hvis du er i tvivl om, hvordan du kan komme i gang med en opgave.
Bemærk: Besvarelsen indeholder ikke selve opgaverne.
Opgave 1 - Plastikbæreposer
1.1
Hvor mange penge har Frida i alt brugt på plastikbæreposer?
14,85 kr.
Gang prisen pr. plastikbærepose med antallet af plastikbæreposer.
Vi beregner, hvor mange penge Frida har brugt på plastikbæreposer:
3 · 4,95 = 14,85
Frida har brugt 14,85 kr. på plastikbæreposer.
Det er vigtigt, at du ikke kun angiver facit, men at du også opstiller et regneudtryk:
3 · 4,95
1.2
Hvor stor en procentdel af prisen på en plastikbærepose skal supermarkedet betale i afgift?
28,1%
(28% godtages også som korrekt svar.)
Beregn, hvor mange procent 1,39 udgør af 4,95.
Vi beregner, hvor mange procent 1,39 kr. udgør af 4,95 kr.:
1,39/4,95 ≈ 0,28081
Supermarkedet skal betale 28,1% af prisen på en plastikbærepose i afgift.
Supermarkedet skal betale 1,39 kr. i afgift, og prisen på en plastikbærepose er 4,95 kr.
Vi omregner resultatet til procent, da opgaven spørger til, hvor stor en procentdel afgiften udgør af prisen. Vi omregner et decimaltal til procent ved at rykke kommaet to pladser mod højre og tilføje et %-tegn.
1.3
Cirka hvor mange penge bruger Fridas familie om året på plastikbæreposer?
2059,20 kr.
Fridas families årlige udgifter til plastikbæreposer kan beregnes på flere måder. Facit i omegnen af 2059,20 kr. godtages også, hvis udregningerne er korrekte.
Beregn først, hvor mange plastikbæreposer Fridas familie køber pr. år.
Vi beregner, hvor mange plastikbæreposer Fridas familie køber om ugen:
2 · 4 = 8
Vi beregner, hvor mange plastikbæreposer Fridas familie køber om året:
8 · 52 = 416
Vi beregner, hvor mange penge Fridas familie bruger på plastikbæreposer om året:
416 · 4,95 ≈ 2059,2
Fridas familie bruger ca. 2059,20 kr. om året på plastikbæreposer.
Vi får oplyst, at Fridas familie i gennemsnit køber 2 plastikbæreposer, hver gang de køber ind, og at de køber ind ca. 4 gange om ugen. Familien køber altså ca. 8 plastikbæreposer om ugen.
Der er ca. 52 uger på et år, så vi kan beregne, hvor mange plastikbæreposer familien køber på et år ved at gange 8 med 52.
Familien køber ca. 416 plastikbæreposer om året. Vi beregner, hvor mange penge Fridas familie bruger på plastikbæreposer ved at gange antallet af plastikbæreposer (416) med prisen pr. pose (4,95 kr.).
1.4
Giv et overslag over, hvor mange poser hver dansker i gennemsnit køber om året.
78 poser
Beregn, hvor mange plastikbæreposer vi laver hvert år i Danmark.
Vi beregner, hvor mange plastikbæreposer, vi laver hvert år i Danmark:
9.000.000.000/20 = 450.000.000
Vi beregner, hvor mange poser hver dansker køber:
450.000.000/5.800.000 ≈ 77,58621
Hver dansker køber i gennemsnit ca. 78 poser om året.
Vi får oplyst, at vi i Danmark laver bæreposer af ca. 9000 tons plastik om året.
1 ton = 1000 kg og 1 kg = 1000 g. Vi omregner 9000 tons til g:
9000 · 1000 · 1000 = 9.000.000.000
Vi laver bæreposer af ca. 9.000.000.000 g plastik om året.
Vi får oplyst, at der skal bruges ca. 20 g plastik til hver pose, så vi beregner, hvor mange poser vi laver om året, ved at dele 9.000.000.000 med 20. Vi laver ca. 450.000.000 poser om året.
Vi får oplyst, at der er ca. 5.800.000 danskere. Vi beregner, hvor mange poser hver dansker i gennemsnit køber, ved at dele 450.000.000 med 5.800.000.
Opgave 2 - Pant for flasker
2.1
Du skal undersøge, hvor mange flasker med pant A, B og C Emil kan have afleveret. Skriv alle de forskellige muligheder der er, når Emil ikke nødvendigvis har afleveret alle de tre slags flasker, som skemaet viser.
Emil kan have afleveret 10 flasker med pant A. Undersøg, om han kan have afleveret 9, 8, 7... osv. flasker med pant A, og hvor mange flasker med hhv. pant B og pant C, han I så fald også har afleveret.
Du kan fx lave en tabel i Excel.
Vi laver en tabel med de forskellige muligheder:
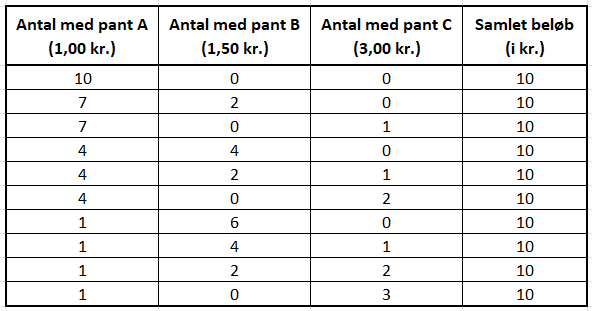
Der er 10 forskellige muligheder.
Emil kan have afleveret 10 flasker med pant A, da pant A flasker giver 1 kr. pr. stk.
Emil kan ikke have afleveret 9 flasker med pant A, da Emil ville få 9 kr. for 9 flasker med pant A. Der mangler 1 kr., for at Emil har fået 10 kr., og aflevering af flasker med pant B eller pant C kan ikke give Emil 1 kr. mere.
Emil kan heller ikke have afleveret 8 flasker med pant A, da Emil så ville få 8 kr., og aflevering af flasker med pant B eller pant C kan ikke give Emil 2 kr. mere.
Hvis Emil afleverer 7 flasker med pant A, så får han 7 kr. Der mangler altså 3 kr., for at Emil har fået 10 kr. Emil kan få 3 kr. ved at aflevere 2 flasker med pant B (1,50 kr. pr. flaske) eller 1 flaske med pant C (3 kr. pr. flaske). Emil kan derfor have afleveret 7 flasker med pant A og 2 flasker med pant B (række 2 i tabellen) eller 7 flasker med pant A og 1 flaske med pant C (række 3 i tabellen).
Vi har brugt samme fremgangsmåde til at komme frem til de andre muligheder.
Opgave 3 - Papirkurve af plastik
3.1
Du skal vise med beregning, at rumfanget af papirkurven er ca. 25.000 cm3.
Rumfanget V af en kasse med længde l, bredde b og højde h kan beregnes med formlen:
V = l · b · h
En samlet papirkurv har form som en kasse, der er 25 cm lang, 25 cm bred og 40 cm høj.
Vi beregner rumfanget:
25 · 25 · 40 = 25000
Rumfanget af papirkurven er ca. 25.000 cm3.
Vi får oplyst, at papirkurven har form som en kasse. Vi aflæser på figuren til højre, at papirkurven er 25 cm lang, 25 cm bred og 40 cm høj.
3.2
Forklar, hvorfor man kan beregne arealet af plastikstykket til en af firmaets papirkurve med formlen i den gule boks.
Opdel plastikstykket i firkanter. Skriv mål på siderne i firkanterne, og beregn arealet af hver firkant.
Plastikstykket består af 5 firkanter: 1 kvadrat med sidelængden s og 4 rektangler med længden h og bredden s.
Arealet af kvadratet (bunden) er s2, mens arealet af hvert rektangel (siderne) er s · h. Der er 4 rektangler, så arealet af alle rektanglerne er 4 · s · h. Det samlede areal er derfor
s2 + 4 · s · h

Plastikstykket består af 5 firkanter: 1 kvadrat i midten og 4 rektangler udenom. Vi har skrevet mål på figurerne: s er sidelængden i bunden, og h er højden.
Vi beregner arealet af en firkant ved at gange længden med bredden. Arealet af kvadratet er derfor s · s, dvs. s2. Arealet af hvert rektangel er s · h. Da der er 4 rektangler, så bliver det samlede areal af rektanglerne 4 · s · h. Vi beregner arealet af hele plastikstykket ved at lægge arealet af kvadratet (s2) sammen med arealet af rektanglerne (4 · s · h):
s2 + 4 · s · h
3.3
Du skal vise med beregning, at arealet af plastikstykket til papirkurven på tegningerne er 4625 cm2.
Sæt sidelængden (25 cm) og højden (40 cm) ind i formlen fra opg. 3.2.
Vi bruger formlen til at beregne arealet:
252 + 4 · 25 · 40 = 4625
Arealet af plastikstykket på tegningerne er 4625 cm2.
Vi bruger formlen fra opg. 3.2:
A = s2 + 4 · s · h
Papirkurven på tegningerne er 40 cm høj. Sidelængden i bunden er 25 cm, så vi sætter s = 25 og h = 40 ind i formlen.
3.4
Undersøg, om det er muligt at fremstille en anden kasseformet papirkurv med kvadratisk bund af et plastikstykke, der er mindre end 4625 cm2, hvis rumfanget skal være mindst 25.000 cm3.
Fx en sidelængde på 26 cm og en højde på 37 cm. Der er mange mulige løsninger.
Prøv dig frem med forskellige mål. Du kan fx lave en tabel i Excel.
Vi prøver os frem med nogle forskellige mål:

Kravene er opfyldt, hvis sidelængden i bunden er 26 cm, og højden er 37 cm.
Vi har lavet en tabel i Excel. Her kan du se de formler, vi har brugt i Excel:

Vi startede med målene på tegningen i opgaven. Derefter gjorde vi sidelængden lidt større og højden lidt mindre. Vi gjorde højden mindre og mindre, indtil vi kom frem til nogle mål, hvor arealet er mindre end 4625 cm2, men rumfanget stadig er større end 25.000 cm3.
Opgave 4 - Plastikproduktion
4.1
Hvor mange tons var plastiskproduktionen større i 2018 end i 1950?
357,5 mio. tons
Husk, at tallene i tabellen er plastikproduktionen i millioner tons.
Vi beregner forskellen mellem plastikproduktionen i 2018 og i 1950:
359 - 1,5 = 357,5
Plastikproduktionen var 357,5 mio. tons større i 2018 end i 1950.
Vi aflæser i tabellen, at verdens plastikproduktion var på 1,5 mio. tons i 1950 og 359 mio. tons i 2018. Vi beregner forskellen ved at trække 1,5 fra 359.
Husk, at tallene i tabellen er plastikproduktionen i millioner tons, dvs. at svaret også er i millioner tons.
4.2
Undersøg, om Frida har ret i sin påstand.
Beregn, hvor stor plastikproduktionen ville have været fra 1950 til 2018, hvis Frida har ret i sin påstand. (Du kan skiftevis lægge 8 år og 9 år til det forrige årstal.)
Vi laver en tabel, hvor vi regner ud, hvor stor plastikproduktionen ville have været igennem årene, hvis den blev fordoblet, hver gang der gik 8,5 år:

Vi sammenligner tallene, som vi har beregnet, med de tal, som vi har aflæst.
Hvis vi ser på hele perioden, så var plastikproduktionen i 2018 næsten lige så stor, som den ville have været, hvis den var blevet fordoblet, hver gang der gik 8,5 år fra 1950. Når vi ser på årene mellem 1950 og 2018, så kan vi se, at det ikke passer ret godt, at produktionen blev fordoblet, hver gang der gik 8,5 år. Fx var plastikproduktionen ikke 12 mio. tons i midten af 1970'erne, men i stedet 50 millioner tons. Plastikproduktionen omkring 1990 og omkring 2000 var også dobbelt så stor, som vi har beregnet, at den ville være. Vi synes ikke, at Frida har ret i sin påstand.
Vi beregner plastikproduktionen i tabellen til venstre ved at lægge skiftevis 8 eller 9 år til det forrige årstal og fordoble produktionen. Fx er produktionen 3 mio. tons i 1958, fordi 1958 er 8 år efter 1950, og produktionen i 1950 var 1,5 mio. tons.
Vi sammenligner de tal, som vi har beregnet, med de tal, som vi har aflæst i tabellen i opgaven.
Det er vigtigt at kigge på hele perioden fra 1950 til 2018, dvs. at det ikke er nok at beregne plastikproduktionen de første år frem til fx 1975 og så lave en konklusion på den baggrund.
Du kan få point for din løsning, uanset om du er enig eller uenig med Frida, så længe du har undersøgt udviklingen i hele perioden og argumenterer for din mening ud fra tallene.
4.3
Viser data i tabellen, at produktionen af plastik fortsat er steget eksponentielt fra 2015 til 2018?
Du kan fx beregne væksten pr. år fra 2015 til 2018, dvs. hvor meget plastikproduktionen er vokset i procent hvert år.
Vi laver en tabel, hvor vi beregner, hvor stor væksten har været hvert år:

Vi kan se, at væksten ikke var den samme hvert år, så produktionen af plastik steg ikke eksponentielt fra 2015 til 2018.
Vi beregner væksten med formlen:
Her er et eksempel, hvor vi beregner væksten fra 2015 til 2016:
Hvis stigningen i plastikproduktionen i procent var den samme hvert år, så ville produktionen være vokset eksponentielt. Da stigningen er på mellem 3,16% og 4,04%, så konkluderer vi, at produktionen ikke steg eksponentielt.
Du kan godt få point for din løsning, selv om du konkluderer, at produktionen steg eksponentielt, så længe du har lavet nogle korrekte beregninger, og du bruger beregningerne til at argumentere for din konklusion.
Opgave 5 - Plastikindsamling
5.1
Hvor mange elever i 10. A samlede mere end 100 stykker plastik ind?
11 elever
Aflæs, hvor mange elever, der samlede mellem 101 og 175 stykker plastik ind.
Vi beregner, hvor mange elever, der samlede mere end 100 stykker plastik ind:
6 + 5 = 11
Der var 11 elever, der samlede mere end 100 stykker plastik ind.
Vi skal beregne, hvor mange elever, der samlede mere end 100 stykker plastik ind, dvs. hvor mange elever, der samlede mindst 101 stykker plastik ind.
Vi aflæser, at der ikke var nogen elever, der samlede mellem 101 og 125 stykker plastik ind. Der var 6 elever, der samlede mellem 126 og 150 stykker plastik ind, og 5 elever, der samlede mellem 151 og 175 stykker plastik ind.
5.2
Cirka hvor mange stykker plastik samlede hver elev i 10. A i gennemsnit ind?
97 stykker
Du kan beregne gennemsnittet med formlen:
Vi beregner gennemsnittet:

Hver elev samlede ca. 97 stykker plastik ind i gennemsnit.
Her kan du se udregningerne:

Vi beregner først interval-midtpunktet for hvert interval. Vi ved ikke præcis hvor mange stykker plastik, hver elev samlede ind, så vi bruger interval-midtpunktet i stedet.
Vi ganger hvert interval-midtpunkt med antallet af elever, så fx er 38 midtpunktet for intervallet [26;50], og der var 6 elever, der samlede mellem 26 og 50 stykker plastik ind, så vi ganger 38 med 6 og får 228.
Vi lægger antallet af elever sammen og får 24, og vi lægger antallet af plastikstykker for hvert interval sammen og får 2337. Der går altså 24 elever i 10. A, og de samlede 2337 stykker plastik ind i alt.
Til sidst bestemmer vi gennemsnittet ved at dele 2337 med 24.
5.3
Undersøg, hvilke ligheder og forskelle der er mellem fordelingen af data fra 10. A og fordelingen af data fra 10. B, og skriv en kort tekst, der forklarer resultatet af din undersøgelse.
Du kan fx sammenligne typeinterval og gennemsnit.
Vi aflæser, hvor mange stykker plastik eleverne i 10. B har indsamlet:

Vi kan se, at der ikke er nogen, der har samlet mere end 175 stykker plastik i begge klasser.
I 10. B var der én elev, der samlede færre end 26 stykker plastik ind, mens alle eleverne i 10. A samlede mindst 26 stykker plastik ind.
Typeintervallet for 10. B er [76;100]. Typeintervallet for 10. A er både [26;50], [51;75] og [126;150].
Vi beregner gennemsnittet for 10. B på samme måde, som vi beregnede gennemsnittet for 10. A:

Gennemsnittet for 10. B er ca. 87 stykker plastik pr. elev, mens gennemsnittet for 10. A er ca. 97 stykker plastik pr. elev. Eleverne i 10. A samlede altså i gennemsnit mere plastik pr. elev.
Vi aflæser på figuren i opgaven, at der var én elev i 10. B, der samlede mellem 0 og 25 stykker plastik ind. På samme måde aflæser vi antallet af elever for hvert af de andre intervaller.
Typeintervallet er det interval, hvor der er flest elever.
Vi bruger tabellen fra opg. 5.2 til at beregne gennemsnittet for 10. B. Vi erstatter antallet af elever i 10. A med antallet af elever i 10. B og får beregnet et gennemsnit på ca. 87 stykker plastik.
Opgave 6 - En trekant i en cirkel
6.1
Tegn en ny trekant i en cirkel på samme måde som Frida.
En diameter i en cirkel er en ret linje, der går fra et tilfældigt punkt på cirkelperiferien, gennem midten af cirklen og ud til cirkelperiferien igen.

Vi har tegnet cirklen og trekanten på samme måde som Frida: Først tegnede vi en cirkel. Derefter tegnede vi en diameter, dvs. en ret linje, der går fra cirkelperiferien gennem cirklens midtpunkt og ud til cirkelperiferien igen.
Til sidst har vi valgt et tilfældigt punkt på cirkelperiferien og tegnet to rette linjer fra punktet og til diameterens endepunkter.
6.2
Forklar, hvorfor både den blå og den gule del af hjælpetegningen er ligebenede trekanter.
En trekant er ligebenet, hvis den har to sider, der er lige lange.
Både den blå og den gule trekant har to sider, hvor det ene endepunkt er i centrum, og det andet endepunkt ligger på cirkelperiferien. De to sider i hver trekant har altså samme længde som cirklens radius. Da de to sider er lige lange, så er trekanterne ligebenede.

De sider, hvor det ene endepunkt er i centrum, og det andet endepunkt er på cirkelperiferien, er markeret med rødt. Cirklens radius er afstanden fra cirklens centrum til cirkelperiferien, så de røde linjer har alle samme længde som radius, dvs. at de er lige lange.
En ligebenet trekant er en trekant, hvor to af siderne er lige lange.
6.3
Forklar, hvorfor udtrykkene i hver af de fire linjer er korrekte.
Linje 1: Den blå og den gule trekant er begge ligebenede.
Linje 2: Vinkelsummen i en trekant er 180°.
Linje 3: Brug linje 1.
Linje 4: Brug ligningen i linje 3. Del med 2.
Linje 1:
Da den blå trekant er ligebenet, så er vinklerne u og w lige store. Da den gule trekant er ligebenet, så er vinklerne s og t lige store.
Linje 2:
Den gule og den blå trekant udgør tilsammen den trekant, som Frida tegnede, hvor vinklerne er u, w + s og t. Vinkelsummen i en trekant er 180°, så
u + w + s + t = 180°
Linje 3:
Da u = w og s = t (linje 1), så kan vi erstatte u med w og t med s i ligningen fra linje 2:
w + w + s + s = 180°
Vi kan omskrive ligningen til
2w + 2s = 180°
Linje 4:
Vi deler med 2 på begge sider af lighedstegnet. Så får vi:
w + s = 90°
Linje 1:
I en ligebenet trekant er to af vinklerne lige store. De to vinkler, der er lige store, er de to vinkler, der ikke ligger mellem de sider, der er lige lange.
I den blå trekant ligger hverken u eller w mellem de to sider, der er lige lange, så u = w. I den gule trekant ligger hverken s eller t mellem de to sider, der er lige lange, så s = t.
Linje 2:
w og s udgør tilsammen den ene vinkel i den trekant, som Frida tegnede. De to andre vinkler er u og t, så vinklerne i Fridas trekant er u, t og w + s. Summen af alle tre vinkler i en trekant er 180°.
Linje 3:
Vi ved fra linje 1, at w = u og s = t, så vi kan erstatte u med w og t med s i ligningen fra linje 2. Da w + w = 2w og s + s = 2s, så får vi ligningen i linje 3.
Linje 4:
Vi deler med 2 på begge sider af lighedstegnet i ligningen i linje 3:
Vi får så:
w + s = 90°
Opgave 7 - En regneopskrift
7.1
Hvad er resultatet i trin 5, hvis starttallet er 4?
22
Du kan fx opstille en tabel ligesom i opgaven og følge regneopskriften trin for trin.
| Trin | Eksempel |
|---|---|
| 1 | 4 |
| 2 | 4, 5, 6, 7 |
| 3 | 6 · 7 = 42 |
| 4 | 4 · 5 = 20 |
| 5 | 42 - 20 = 22 |
Trin 1: Starttallet er 4.
Trin 2: De tre efterfølgende hele tal er 5, 6, og 7.
Trin 3: De to største tal i trin 2 er 6 og 7.
Trin 4: De to mindste tal i trin 2 er 4 og 5.
Trin 5: Vi trækker resultatet i trin 4 (dvs. 20) fra resultatet i trin 3 (dvs. 42).
7.2
Du skal vise med beregning, at hvis starttallet er 7, så er summen af de fire tal i trin 2 lig med resultatet i trin 5.
Følg regneopskriften med starttallet 7. Beregn derefter summen af de fire tal i trin 2.
| Trin | Eksempel |
|---|---|
| 1 | 7 |
| 2 | 7, 8, 9, 10 |
| 3 | 9 · 10 = 90 |
| 4 | 7 · 8 = 56 |
| 5 | 90 - 56 = 34 |
Summen af tallene i trin 2 er:
7 + 8 + 9 + 10 = 34
Summen af de fire tal i trin 2 er lig med resultatet i trin 5.
Trin 1: Starttallet er 7.
Trin 2: De tre efterfølgende hele tal er 8, 9 og 10.
Trin 3: De to største tal i trin 2 er 9 og 10.
Trin 4: De to mindste tal i trin 2 er 7 og 8.
Trin 5: Vi trækker resultatet i trin 4 (dvs. 56) fra resultatet i trin 3 (dvs. 90).
Vi lægger de fire tal i trin 2 sammen. Til sidst konkluderer vi, at summen af de fire tal er den samme som resultatet i trin 5.
7.3
Forklar, hvorfor man kan skrive summen af de fire tal i trin 2 som n + (n + 1) + (n + 2) + (n + 3), hvis starttallet er n.
De fire tal i trin 2 er starttallet og de tre efterfølgende tal. De tre efterfølgende tal er 1 større, 2 større og 3 større end starttallet.
Tallene i trin 2 er starttallet og de tre efterfølgende tal, dvs.
- det tal, der er 1 større
- det tal, der er 2 større
- det tal, der er 3 større
Hvis n er starttallet, så er de efterfølgende tal derfor n + 1, n + 2 og n + 3. Summen af de fire tal i trin 2 er derfor n + (n + 1) + (n + 2) + (n + 3).
Tallet, der er 1 større end n, er n + 1.
Tallet, der er 2 større end n, er n + 2.
Tallet, der er 3 større end n, er n + 3.
7.4
Bevis, at resultatet i trin 5 er lig med summen af de fire tal i trin 2, ligegyldigt hvilket starttal man vælger.
Omskriv summen fra opg. 7.3.
Omskriv udtrykket i den blå boks.
Vi beregner summen af de fire tal fra opg. 7.3.
n + (n + 1) + (n + 2) + (n + 3) = 4n + 6
Vi omskriver udtrykket i den blå boks:
(n + 3) · (n + 2) - (n + 1) · n = 4n + 6
De to udtryk er ens, så resultatet i trin 5 er lig med summen af de fire tal i trin 2, uanset hvad starttallet er.
Du kan omskrive summen af de fire tal og udtrykket i den blå boks "i hånden" eller ved at bruge et CAS-værktøj, fx GeoGebra™. Du kan omskrive udtrykkene i GeoGebra ved at taste udtrykkene ind i CAS-vinduet.
Opgave 8 - To lige store dele
8.1
Lav præcise tegninger af de fem figurer herunder, og undersøg, hvordan du kan dele hver af dem i to lige store dele med ét linjestykke. Du skal kun vise én løsning for hver figur.
Nogle figurer kan opdeles i to mindre figurer, der er kongruente.


Rektangel
Vi opdeler rektanglet i to mindre rektangler, der hver har længden 3 og bredden 2, dvs. at de to små rektangler er lige store.
Parallelogram
Vi tegner en diagonal i parallelogrammet. Diagonalen opdeler figuren i to trekanter, hvor siderne er parvist lige lange, dvs. at de to trekanter er lige store.
Trapez

Arealet af et trapez beregnes ud fra længden af de parallele sider (a og b) og højden (h):
Vi opdeler trapezet i to mindre trapezer, hvor de to parallelle linjer er parvist lige lange, og hvor højden er den samme. De to trapezer er derfor lige store.
Trekant
Arealet af en trekant beregnes ud fra højden (h) og grundlinjen (g):
Vi opdeler trekanten i to mindre trekanter, hvor højden er den samme, og hvor grundlinjerne er lige lange. De to trekanter er derfor lige store.
Figuren bestående af to rektangler og en trekant
Begge rektangler har bredden 2. Det ene rektangel har længden 4, dvs. at arealet er 8. Det andet rektangel har længden 5, dvs. at arealet er 10.
I trekanten er længden af den ene grundlinje 3, og den tilhørende højde har længden 4. Vi beregner arealet:
Arealet af trekanten er 6.
Vi opdeler trekanten i to mindre trekanter, der har samme højde (med længden 4). I den ene trekant har grundlinjen længden 1, dvs. at arealet er 2. I den anden trekant har grundlinjen længden 2, dvs. at arealet er 4.
Arealet af den ene del af figuren er dermed
10 + 2 = 12
Arealet af den anden del af figuren er
8 + 4 = 12


![\begin{align*} \frac{335-322}{322} &\approx 0,0404 \\[1em] &\approx 4,04% \end{align}](/media/webbooks/3942/49956/images/equations/qzlimqt7rnawknl76eqqew==.svg)




