Stykkevis lineær funktion
Gaffelforskrift
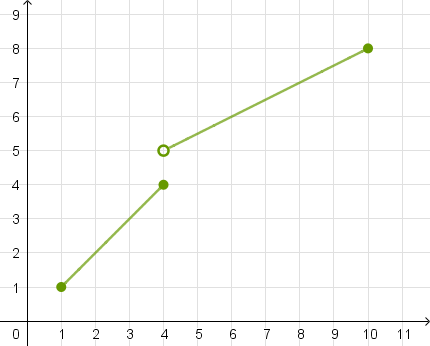
Figuren herover viser graferne for to funktioner g og h. Husk på, at symbolet "○" betyder, at punktet ikke ligger på grafen, mens symbolet "●" betyder, at punktet ligger på grafen.
Funktionerne g og h er givet ved:
Vi kan også betragte linjestykkerne som grafen for én funktion f, hvor funktionsværdien bestemmes som x eller 
Forskriften kaldes en gaffelforskrift.
Forskriften for f viser, at hvis 1 ≤ x ≤ 4, så er funktionsværdien lig med x. Hvis 4 < x ≤ 10, så er funktionsværdien 


En gaffelforskrift kan bestå af mere end to delfunktioner. Herunder kan du se et eksempel med tre delfunktioner.

Bemærk: Vi kan kun betragte flere linjestykker og/eller halvlinjer som én graf, hvis de er defineret på intervaller, der ikke overlapper. Ét af kendetegnene ved en funktion er, at funktionsværdien er entydig, dvs. at til enhver værdi af x hører kun én funktionsværdi. Hvis intervallerne overlapper hinanden, så kan vi ikke aflæse en entydig funktionsværdi, og dermed er der ikke tale om en funktion. Du kan se et eksempel herunder, hvor vi kan aflæse...

![\begin{align*} &g(x) = x, \quad 1 \leq x \leq 4 \\[1em] &h(x) = \frac{1}{2}x + 3, \quad 4 < x \leq 10 \end{align*}](https://media.studienet.dk/files/webbooks/images/1981/equations/5QlLm1e7xHo9T2lsKYtIJA==.svg)
![\begin{align*} f(x) = \left\{\begin{matrix} x, & 1 \leq x \leq 4 \\[1em] \dfrac{1}{2}x + 3, & 4 < x \leq 10 \end{matrix}\right. \end{align*}](https://media.studienet.dk/files/webbooks/images/1981/equations/kCnUlKC9cv-RfVEy0Sd2wQ==.svg)
