Matematik A HTX - 24. maj 2023
Her er vores besvarelse af opgaverne fra den skriftlige eksamen i Matematik A på HTX d. 24. maj 2023.
Besvarelsen indeholder opgavernes facit og vores løsninger. Løsningerne til opgaverne i delprøve 1 er lavet i to versioner:
- den ene version er lavet, så den ligner en eksamensbesvarelse
- den anden version indeholder ekstra forklaringer og henvisninger til de formler i formelsamlingen, som vi har brugt.
Løsningerne til opgaverne i delprøve 2 er lavet med CAS-værktøjet WordMat.
Bemærk: Besvarelsen indeholder ikke selve opgaverne.
Delprøve 1
Den første delprøve består af følgende opgaver:
1a) Udfyld de manglende pladser i tabellen, benyt eventuelt bilag 1.
2a) Tegn tangenten til grafen for g i punktet P(1;1). Bilag 2 kan benyttes.
2b) Bestem en ligning for tangenten til grafen for g i P.
3a) Bestem koordinaterne for enhedsvektoren i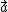 
's retning.
4a) Hvor stor en del af kassens volumen optages af keglen?
Delprøve 2
Den anden delprøve består af følgende opgaver:
5a) Bestem lampens højde h, se figur 4.
5b) Bestem i hvilket punkt grafen for har en tangent med hældningen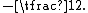 
6a) Bestem arealet af cirkelringen.
6b) Vis at den ydre cirkel c1 kan beskrives ved ligningen (x - 38)2 + (y - 18)2 = 17,52.
6c) Vis at B har koordinaterne (22,0;25,1), når resultatet angives med en decimals nøjagtighed.
6d) Bestem vinklen v, se figur 5.
7a) Angiv sfd(1008,210) ud fra figur 6.
7b) Gør rede for hvordan tallene 4 og 168 i øverste linje fremkommer.
7c) Benyt sætning 2 og sætning 3 i forberedelsesmaterialet til at forklare hvorfor sfd(1008,210) = sfd(210,168) = sfd(168,42) = sfd(42,0) = 42. (Vi har ikke løst opgaven.)
8a) Bestem væksthastigheden for en labrador, der vejer 6 kg.
8b) Hvor gammel er labradoren, når den vejer 25 kg ifølge modellen?
8c) Tegn grafen for N sammen med datasættet og kommentér.
Eksamenskode: htx231-MAT/A-24052023
