Rødder i andengradspolynomier

Indhold

Bestem rødderne med nulpunktsformlen
Aflæs rødder i forskrift

Bestem rødderne med nulpunktsformlen

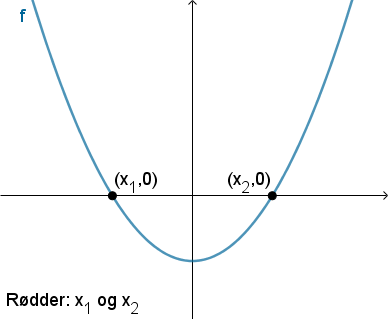
Rødderne i et andengradspolynomium er førstekoordinaterne til parablens skæringspunkter med x-aksen. Vi bestemmer derfor rødderne ved at løse ligningen f(x) = 0. Da f(x) = ax2 + bx + c, så finder vi rødderne x1 og x2 ved at løse andengradsligningen

ax2 + bx + c = 0

Sætning. Nulpunktsformel.

Fortegnet for diskriminanten d = b2 - 4ac angiver antallet af rødder i andengradspolynomiet f(x) = ax2 + bx + c:

Hvis d > 0, så har polynomiet 2 rødder. Rødderne er givet ved

$x_1 = \frac{-b - \sqrt{d}}{2a} \quad \text{ og } \quad x_2 = \frac{-b + \sqrt{d}}{2a}$

Hvis d = 0, så har polynomiet én rod. Roden er givet ved

$x = \frac{-b}{2a}$

Hvis d < 0, så har polynomiet ingen rødder.

Du finder et bevis for nulpunktsformlen på siden Bevis for rødderne i et andengradspolynomium.

Eksempel: Bestem rødderne (to rødder)

Andengradspolynomiet f er givet ved

f(x) = 2x2 - 2x - 4

Vi bestemmer diskriminanten:

$\begin{align*} d &= (-2)^2 - 4 \cdot 2 \cdot (-4) \\[1em] &= 4 + 32 \\[1em] &= 36 \end{align*}$

Da d > 0...