Bestem vinkler og sidelængder i en trekant
Du kan benytte denne vejledning, hvis du kender nogle af vinklerne og længden af nogle af siderne i en trekant eller en figur bestående af trekanter, og du skal beregne
- en eller flere vinkler
- længden af en eller flere sider, medianer, højder eller vinkelhalveringslinjer
- omkredsen af figuren
...
Eksempler på opgaveformuleringer
- Bestem vinkel A i trekant ACF.
- Bestem ∠CDE og længden af siden DE.
- Bestem længden af hA.
- Bestem længden af vinkelhalveringslinjen fra vinkel E.
- Bestem længden af medianen fra F.
- Bestem |AE| og længden af hypotenusen i trekant ADE.
- Bestem omkredsen af trekant ACD.
I denne vejledning viser vi, hvordan du kan benytte en trekantsberegner/trekantsløser til at beregne vinkler og sidelængder.
...
Metode
1. Afgør hvilken vinkel eller sidelængde, du skal bestemme
Som det første skal du identificere den vinkel eller sidelængde, som du skal bestemme. I nogle opgaver er der vist en tegning eller skitse af figuren. Hvis ikke det er tilfældet, så anbefaler vi, at du tegner en skitse for at få et overblik over opgaven.
Når du løser opgaver, hvor der er givet en tegning, så kan det være nødvendigt at tilføje linjestykker og vinkler til tegningen, hvis du fx skal bestemme længden af en vinkelhalveringslinje, median eller højde, der ikke er vist på tegningen.
2. Identificér de oplysninger, der er givet i opgaven
Når du skal bestemme en vinkel eller længden af en …
...
Eksempel: Beregn vinkel B
I en trekant ABC er |AB| = 6 og |AC| = 8. Vinkel A er 36°. Beregn vinkel B i trekant ABC.
Kun brugere med et Studienet medlemskab kan se dette indhold. Køb adgang.
Kun brugere med et Studienet medlemskab kan se dette indhold. Køb adgang.
...
Eksempel: Bestem vinkel A og vinkel C
På figuren ses trekant ABC. Nogle mål er opgivet på figuren. Vinkelhalveringslinjen gennem vinkel B skærer siden AC i punktet D. Længden af vinkelhalveringslinjen er 4,34. Det oplyses at vinkel C er stump. Bestem vinkel A og vinkel C.
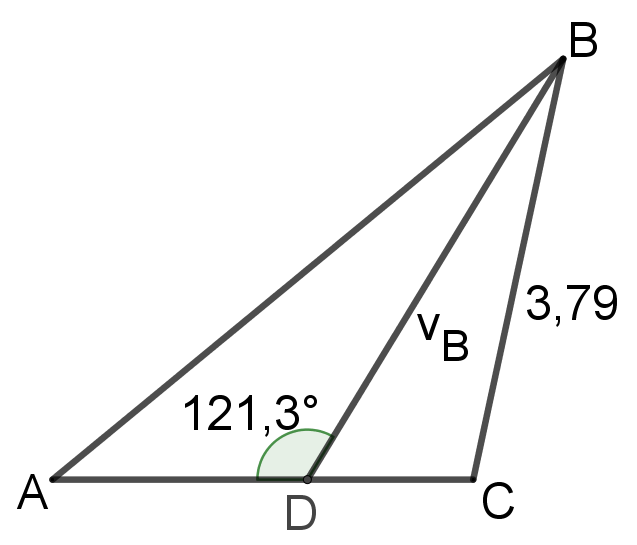
Kun brugere med et Studienet medlemskab kan se dette indhold. Køb adgang.
Kun brugere med et Studienet medlemskab kan se dette indhold. Køb adgang.
...
Opgaver, du kan øve dig på
Du kan finde opgaver, som du kan øve dig på, i Vejledende Enkeltopgaver HF C. Selv om du ikke går på HF, så kan du godt bruge opgaverne til at øve dig.
Du kan finde opgaverne på emu.dk og vores besvarelser her:

