Lav en følsomhedsanalyse
En følsomhedsanalyse bruges til at undersøge, hvor meget den ene af koefficienterne i kriteriefunktionen f(x,y) = ax + by kan ændres, uden at det ændrer på den optimale løsning.
Ofte vil kriteriefunktionen beskrive en virksomheds samlede dækningsbidrag ved salg af to produkter, hvor koefficienterne a og b er dækningsbidraget pr. enhed af hhv. det ene og det andet produkt. Opgaven går i så fald ud på at undersøge, hvor meget dækningsbidraget for det ene produkt kan ændres, uden at den optimale produktsammensætning ændres.…
...
Eksempler på opgaveformuleringer
Herunder er der tre eksempler på opgaver, der kan besvares ved at lave en følsomhedsanalyse.
- Bestem hvor meget dækningsbidraget pr. Super Salatmix kan stige, uden at det ændrer på den optimale løsning fra spørgsmål a).
- Bestem det interval, som dækningsbidraget for produkt A skal ligge i, hvis løsningen fra opgave b) fortsat skal være den optimale.
- Bestem hvor meget dækningsbidraget for Type I skal falde, før virksomheden udelukkende bør producere Type II.…
...
Metode
1. Identificér kriteriefunktionen og det hjørne, hvor kriteriefunktionen antager sin optimale værdi
Kriteriefunktionen er en lineær funktion af to variable, dvs. at den er på formen f(x,y) = ax + by. Du vil typisk have arbejdet med kriteriefunktionen i en tidligere delopgave, hvor du har fundet den optimale løsning, dvs. det hjørne i polygonområdet, hvis koordinater minimerer eller maksimerer kriteriefunktionen (alt efter hvad der bliver spurgt til).
Når du skal lave en følsomhedsanalyse, så skal du kende…
...
Eksempel: Den optimale løsning ligger ikke på en akse
En virksomhed producerer og sælger to produkter, vinterdæk og sommerdæk. Dækningsbidraget (i kr.) ved salg af de to produkter kan beskrives med funktionen DB(x,y) = 3x + 4y, hvor x er antal solgte vinterdæk og y er antal solgte sommerdæk.
Produktionen er underlagt følgende begrænsninger
x + y ≤ 50
x + 3y ≤ 90
x ≥ 0
y ≥ 0
Virksomheden opnår det størst mulige dækningsbidrag, når der produceres og sælges 30 vinterdæk og 20 sommerdæk. På figuren herunder er polygonområdet og niveaulinjen N(170) tegnet i samme koordinatsystem.
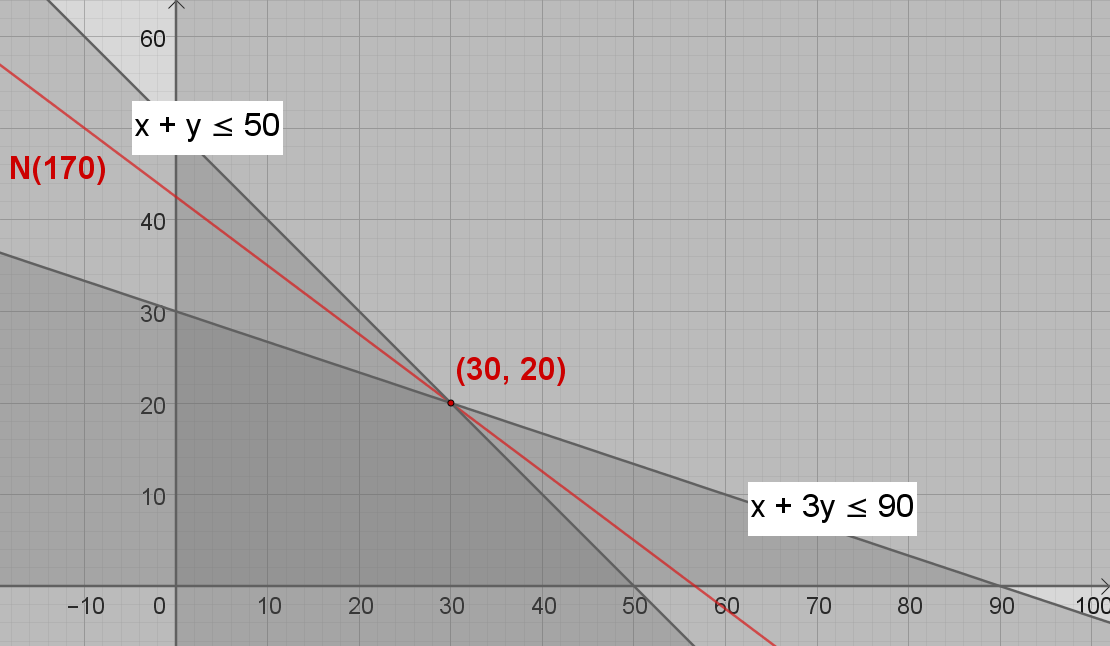
Bestem, hvor meget dækningsbidraget for vinterdæk må stige, hvis den optimale produktsammensætning fortsat skal være den samme.
Kun brugere med et Studienet medlemskab kan se dette indhold. Køb adgang.
Kun brugere med et Studienet medlemskab kan se dette indhold. Køb adgang.
…...
Eksempel: Den optimale løsning ligger på y-aksen
En virksomhed producerer og sælger to produkter. Funktionen f(x,y) = 2x + 7y beskriver virksomhedens dækningsbidrag (i kr.), når der sælges x enheder af produkt 1 og y enheder af produkt 2.
Virksomhedens produktion og salg er underlagt en række begrænsninger:
2x + 5y ≤ 14000
2x + 3y ≤ 12000
x ≥ 0
y ≥ 0
Det oplyses, at virksomhedens dækningsbidrag bliver størst muligt, når der sælges 0 enheder af produkt 1 og 2800 enheder af produkt 2. Figuren herunder viser polygonområdet og niveaulinjen N(19600), der tangerer polygonområdet i punktet (0,2800).
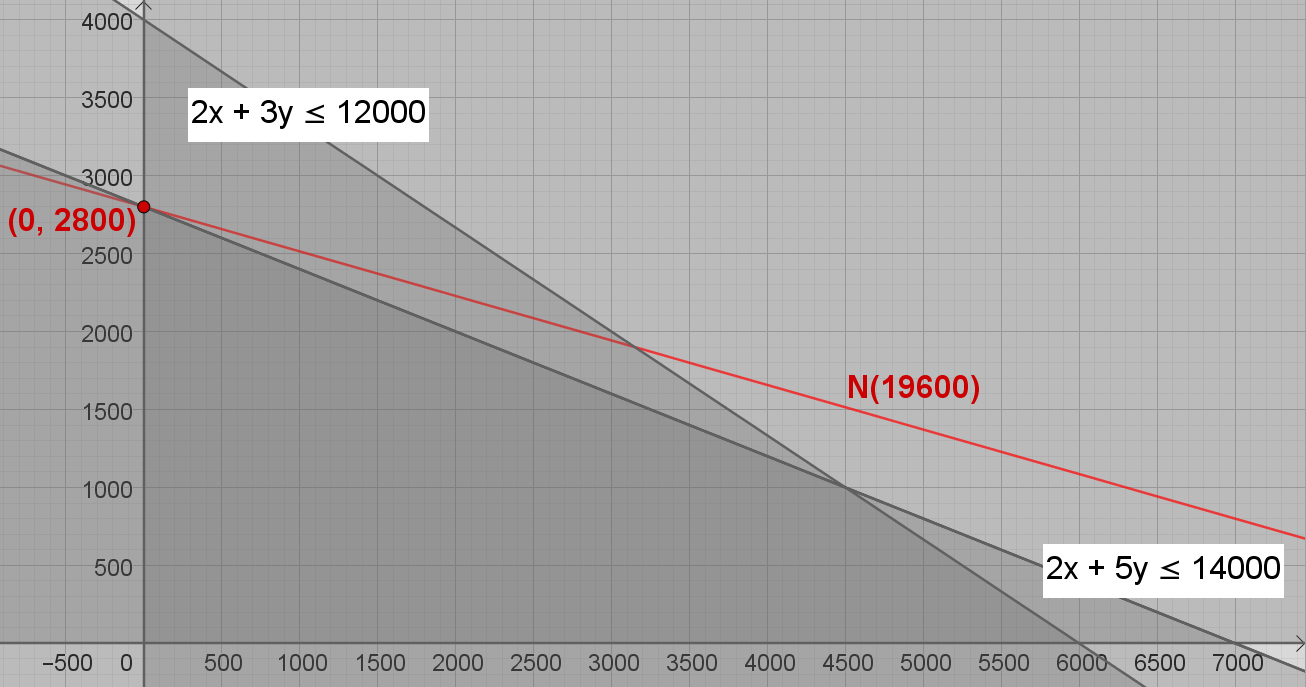
Bestem, hvor stort dækningsbidraget for produkt 2 skal være, for at det er optimalt for virksomheden at producere 0 enheder af produkt 1 og 2800 enheder af produkt 2.
Kun brugere med et Studienet medlemskab kan se dette indhold. Køb adgang.
Kun brugere med et Studienet medlemskab kan se dette indhold. Køb adgang.
…
