Matematik A HTX - 24. maj 2022

Her er vores besvarelse af opgaverne fra den skriftlige eksamen i Matematik A på HTX d. 24. maj 2022.

Besvarelsen indeholder opgavernes facit og vores løsninger. Løsningerne til opgaverne i delprøve 1 er lavet i to versioner:

• den ene version er lavet, så den ligner en eksamensbesvarelse
• den anden version indeholder ekstra forklaringer og henvisninger til de formler i formelsamlingen, som vi har brugt.

Løsningerne til opgaverne i delprøve 2 er lavet med CAS-værktøjet WordMat.

Bemærk: Besvarelsen indeholder ikke selve opgaverne.

Delprøve 1

Den første delprøve består af følgende opgaver:

1a) Bestem de kartesiske koordinater for 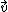og , samt for .

2a) Bestem en forskrift for den stamfunktion F til f, som opfylder at F(0) = 5.

3a) Reducér nedenstående udtryk mest muligt 2 · (a + b)² + (5a + b) · (a - b).

4a) Argumentér for at |OA| , |OB| og |OC| er lige store.

4b) Argumentér for at ABC er retvinklet.

Delprøve 2

Den anden delprøve består af følgende opgaver:

5a) Vis at B og C har koordinaterne B(0;4;0) og C(0;0;5).

5b) Vis at en ligning for α er givet ved 10x + 15y + 12z = 60.

5c) Bestem afstanden fra origo O til α.

6a) Indtegn data i et koordinatsystem.

6b) Bestem a og b.

6c) Hvilken rotordiameter har vindmøllen ifølge din model?

6d) Afgør om påstanden passer med din model.

7a) Vis at sidelængden l ≈ 1,18, se figur 5.

7b) Vis at vinkel v ≈ 96,3°, se figur 5.

7c) Bestem arealet af det øverste vindue.

8a) Bestem arealet A for x = 2.

8b) Opstil rekursionsligningen, der anvender Newtons metode til at finde nulpunkt for funktionen B(x) = A(x) - 0,7.

8c) Anvend startgættet x₀ = 3 og brug Newtons metode til at bestemme x₁, x₂, x₃ og x₄ ved hjælp af et IT-værktøj. Kommentér resultatet.

9a) Argumentér for at den kage der bliver spist, kan beskrives ved den uendelige række

9b) Bestem de første 5 elementer i den tilsvarende afsnitsfølge (s_n) og indtegn dem i et (n,s)−koordinatsystem.

9c) Argumentér for at rækken er konvergent, og angiv hvor meget af othellolagkagen Alma og Benjamin tilsammen får spist.

Eksamenskode: htx221-MAT/A-24052022