Potensvækst
Egenskaber ved potensvækst
Potensfunktioner er givet ved en forskrift af typen f(x) = b · xa. Når x bliver k gange så stor, så bliver funktionsværdien ka gange så stor.
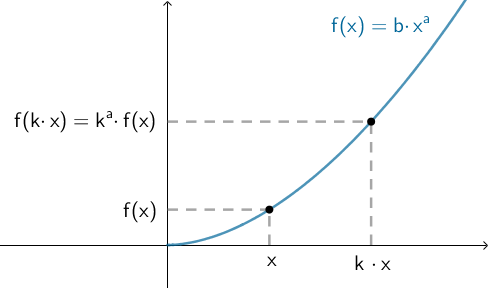
At gange x med k svarer til at x ændres med en procentsats, rx. Tilsvarende svarer det, at gange funktionsværdien med faktoren ka, til at funktionsværdien ændres med en procentsats, ry.
Vi bestemmer den relative tilvækst i x-værdien, rx:
 | = |  |
| = |  |
Da rx = k - 1, så er k = 1 + rx.
Derefter bestemmer vi funktionsværdien f(k · x):
 | = |  |
| = |  | |
| = |  | |
| = |  | |
| = |  |
Den relative tilvækst i funktionsværdien, ry, er dermed
 | = |  |
| = |  | |
| = |  |
Sammenhængen mellem den relative tilvækst i x-værdien og den relative tilvækst i funktionsværdien er altså
1 + ry = (1 + rx)a
Når den uafhængige variabel, x, vokser med en fast procentsats, rx, så vokse...

