Andengradspolynomier
Indhold
Forskrift
- Et andengradspolynomium er en funktion på formen
- Eksempel: Funktionen f(x) = 2x2 + 3x - 4 er et andengradspolynomium.
Grafen er en parabel
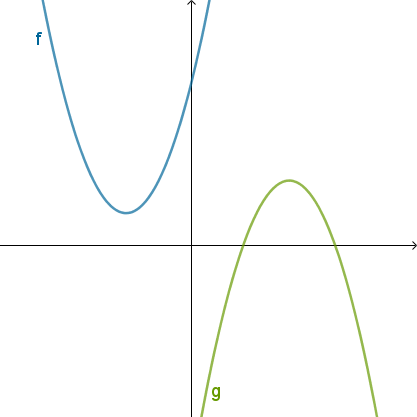
- Grafen for et andengradspolynomium kaldes en parabel. En parabel er buet og buer enten opad eller nedad.
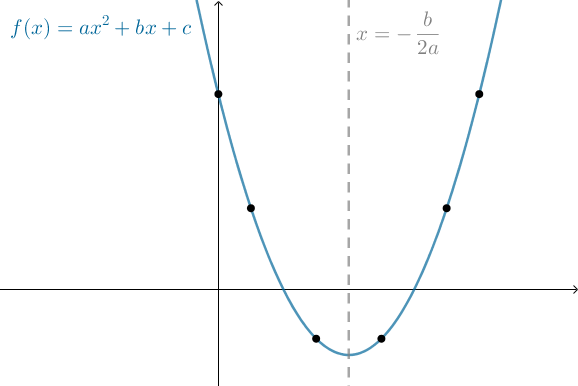
- En parabel er symmetrisk omkring en symmetrilinje givet ved
Symmetrilinjen deler grafen op i to dele, der kaldes parablens grene eller ben.
Toppunkt
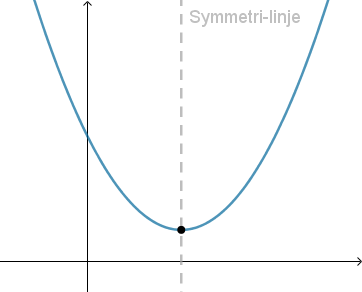
- Skæringspunktet mellem en parabel og dens symmetrilinje kaldes parablens toppunkt.
- Toppunktet T på den parabel, der er graf for andengradspolynomiet f(x) = ax2 + bx + c, har koordinaterne
hvor d = b2 - 4ac. Tallet d kaldes diskriminanten.
- Eksempel: En funktion f er givet ved f(x) = x2 + 2x - 3. Vi bestemmer diskriminanten:
Derefter bestemmer vi toppunktets koordinater:
Toppunktets koordinater e



![\begin{align*} d &= 2^2 - 4 \cdot 1 \cdot (-3) \\[0.5em] &= 16 \end{align}](https://media.studienet.dk/files/webbooks/images/1981/equations/sSH2acihzti_3o-YC5wIBg==.svg)
![\begin{align*} T &= \left ( -\frac{2}{2\cdot 1}, -\frac{16}{4 \cdot 1} \right ) \\[0.5em] &= \left ( -1, -4 \right ) \end{align}](https://media.studienet.dk/files/webbooks/images/1981/equations/QbRodhDljid-MgobazVTHQ==.svg)
