Bevis for halveringskonstanten
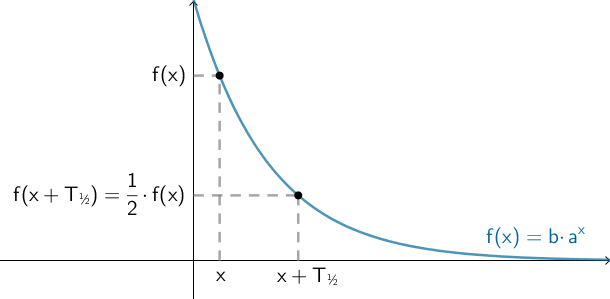
Her beviser vi formlen for halveringskonstanten T½:
Enhver eksponentielt aftagende funktion har en halveringskonstant. Halveringskonstanten er den værdi, som vi skal lægge til x, for at funktionsværdien bliver halveret, dvs. at
Vi gennemgår et eksempel, hvor vi bestemmer en halveringskonstant,...



