Differenskvotient, differentialkvotient og differentiabilitet
Indhold
Differentialkvotient
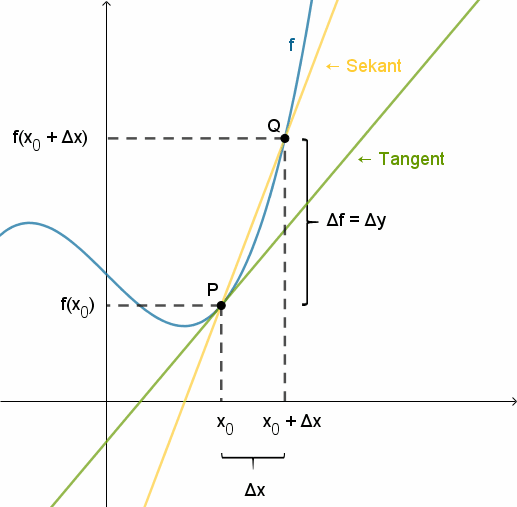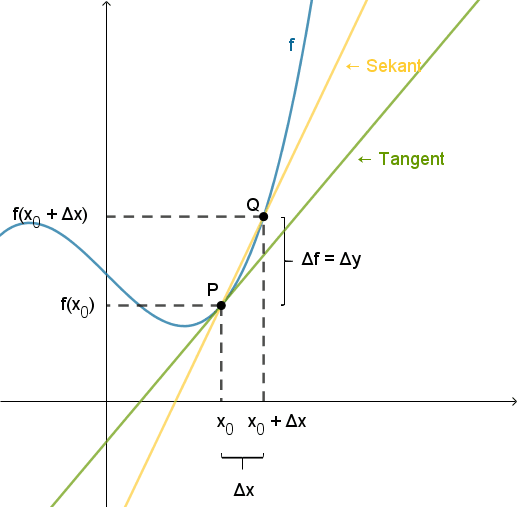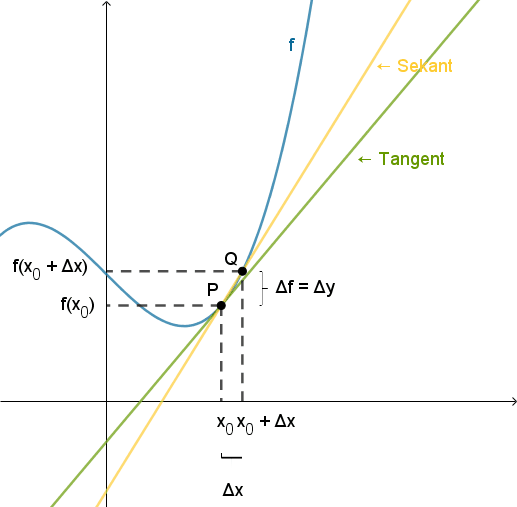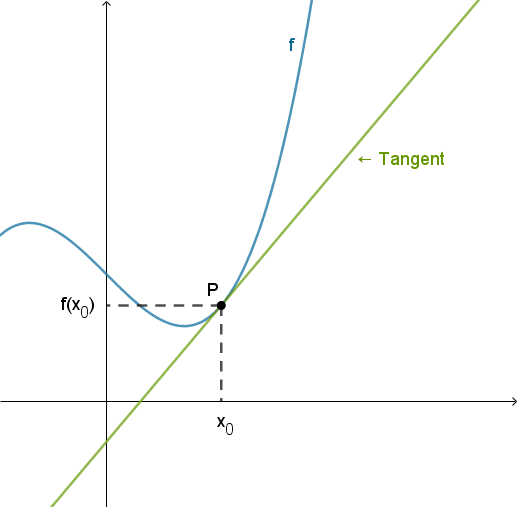
- Differentialkvotienten i x0 skrives f '(x0).
- Differentialkvotienten er grænseværdien for differenskvotienten, når Δx går mod 0 (dvs. når Q nærmer sig P):
- Differentialkvotienten er tangentens hældning.
- Hvis differentialkvotienten i x0 findes, dvs. hvis differenskvotienten har en grænseværdi, så siger vi, at f er differentiabel i x0.
- Differentialkvotienten kan fortolkes som den øjeblikkelige væksthastighed.
- Du kan få hjælp til at løse opgaver, hvor du skal bestemme en differentialkvotient eller fortolke en differentialkvotient, i vejledningen Bestem og forklar betydningen af en differentialkvotient.
Differenskvotient

- Differenskvotienten for f er hældningen på sekanten (den gule linje gennem P og Q):
Δf = f(x0 + Δx) - f(x0) kaldes funktionstilvæksten.



