Bevis for middelværdisætningen
Middelværdisætningen
Middelværdisætningen.
Hvis en funktion f er kontinuert i det lukkede interval [a,b] og differentiabel i det åbne interval ]a,b[, så findes der et tal c i ]a,b[, så
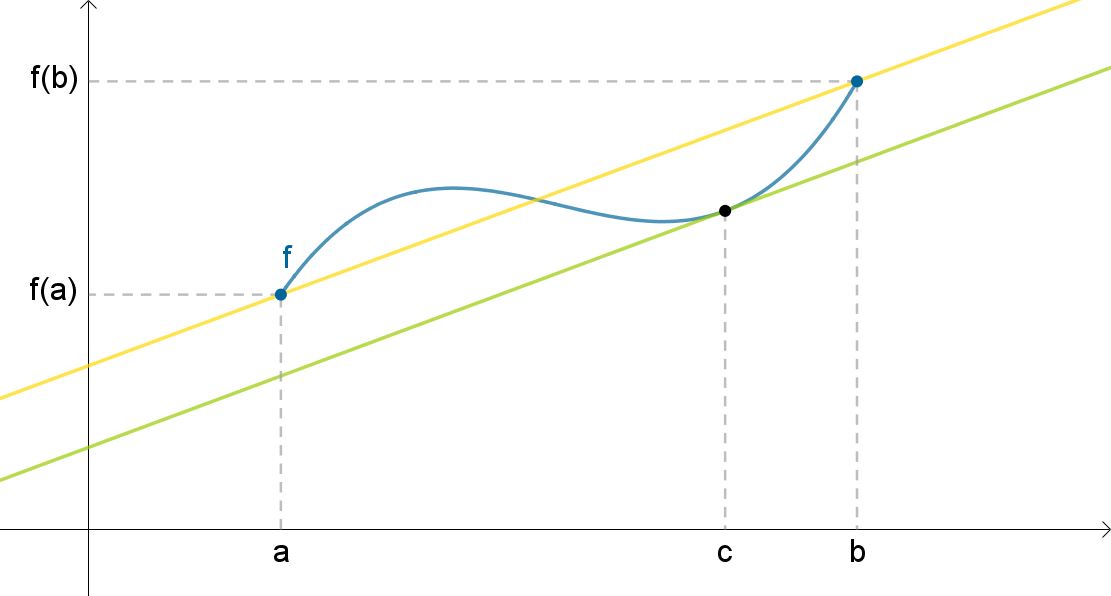
Den geometriske fortolkning af middelværdisætningen er, at der findes et tal c mellem a og b, så tangenten til grafen for f i (c, f(c)) har samme hældning som sekanten gennem (a, f(a)) og (b, f(b)). På figuren herover er den grønne linje tangenten. Den gule linje er sekanten.
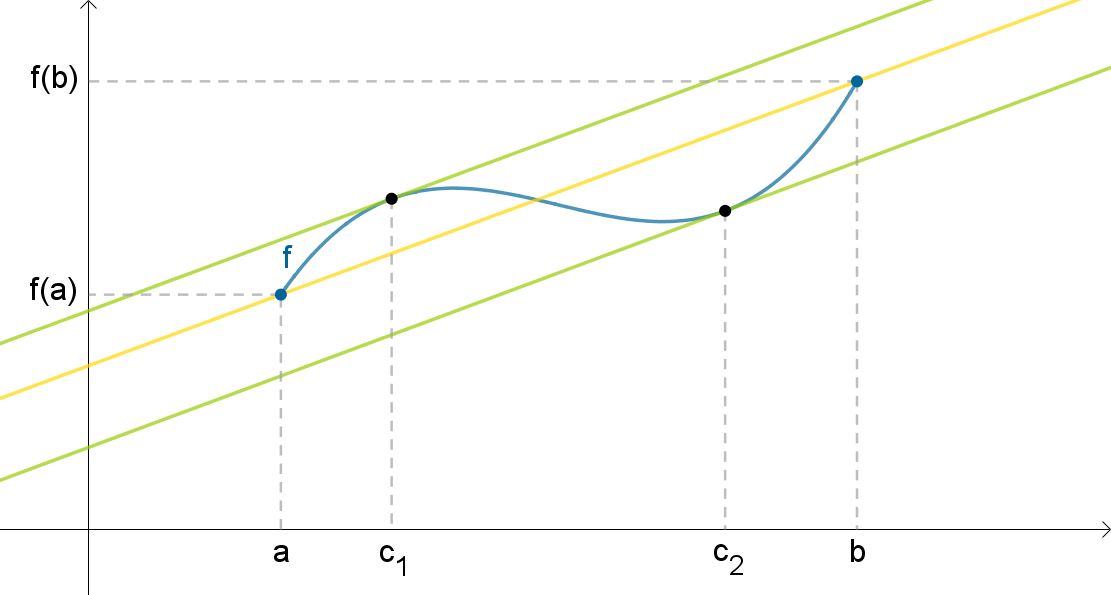
Læg mærke til, at sætningen ikke siger noget om, hvor mange tal c, der findes, men blot at der findes mindst ét. I eksemplet på figuren herunder, har vi markeret to værdier, der opfylder betingelsen.
Bevis
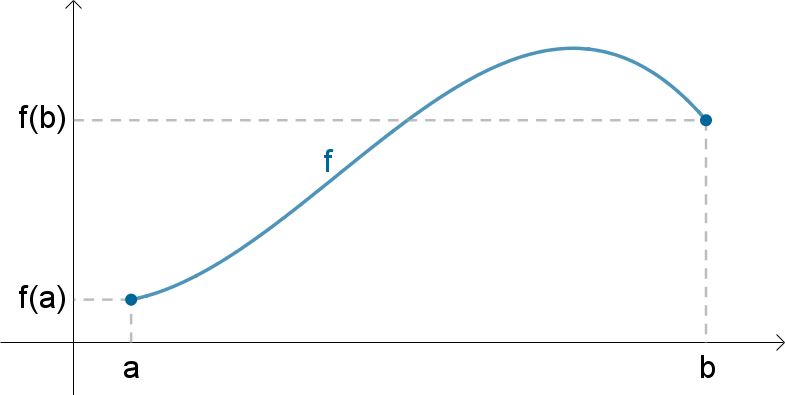
Vi lader f være en funktion, der er kontinuert i det lukkede interval [a,b] og differentiabel i det åbne interval ]a,b[.
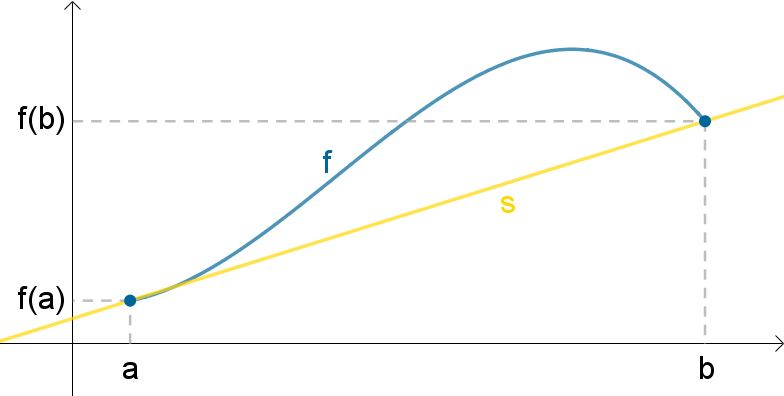
Grafen for f har en sekant gennem punkterne (a,f(a)) og (b,f(b...
